To understand matrix equations, you should know how to multiply two matrices. Let's say you are showed the result of two matrices multiplication (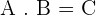 $\text{[math]}$ ) and you are asked to find the matrix B and you are provided matrix A and C, how will you find it? With the help of the matrix equation. In a matrix equation, the unknown is a matrix. This means that you will denote the unknown matrix as matrix X.

A · X = B

To solve, check that the matrix is invertible, if it is, premultiply (multiply to the left) both sides by the matrix inverse of A.

If the equation is of type X · A = B, the members must postmultiply (multiply to the right) because matrix multiplication is not commutative.

1. Given the matrices 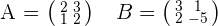$\text{[math]}$ . Solve the equation: A · X = B

$\text{[math]}$

Find the determinant of the above matrix.

$\text{[math]}$ $\text{[math]}$

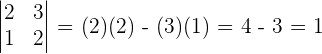
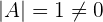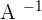
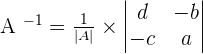
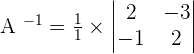
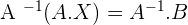
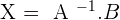
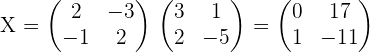
$\text{[math]}$ , this means that there is an inverse $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

2. Given the matrices 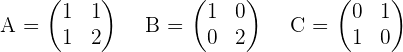$\text{[math]}$ . Solve the equation: X · A + B = C

$\text{[math]}$ $\text{[math]}$

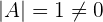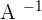
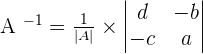
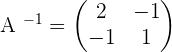
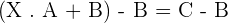
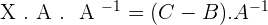
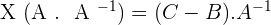
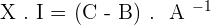
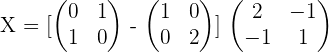
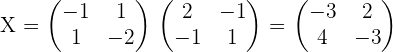
$\text{[math]}$ , this means that there is an inverse $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

$\text{[math]}$

3.Solve the matrix equation:

A · X + 2 · B = 3 · C

$\text{[math]}$

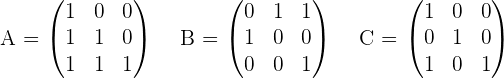
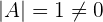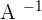
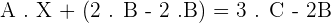
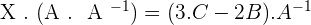
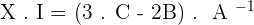
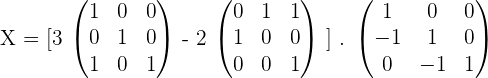
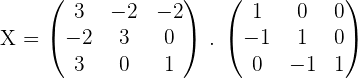
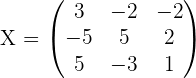
$\text{[math]}$ , this means that there is an inverse $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

4.Solve the matrix equation:

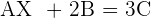
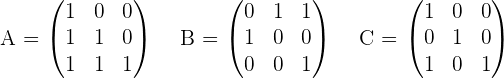
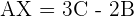
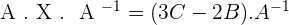
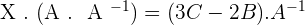
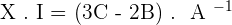
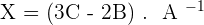
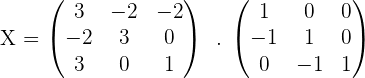
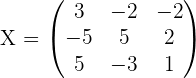
$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

To solve a system of linear equations, it can be transformed into a matrix equation and then solved.

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Did you like this article? Rate it!

4.00 (11 rating(s))

Emma

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Leave us a comment

Cancel reply

Little p

March 2025

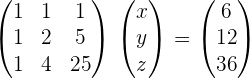
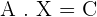
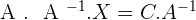
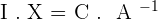
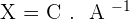
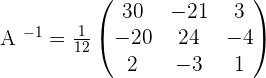
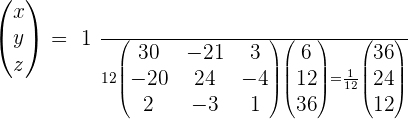
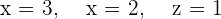
I appreciate your work, thanks so much keep up the good work ✅

Vanessa

April 2025

Hello Little P! Thanks very much for the positive feedback!

hariz

January 2025

I didn’t get the same answer for the second question, ive also asked my friends and we all got the same answer it just didnt line up with yours. Apart from that, great website and thanks for the exercises.

Abhishek Lawaniya

August 2024

Very nice and good explanation of matrix
Give some more examples of matrix

Bakhat Ali

July 2024

I want to more study about matrix that’s why I’m using Google

Matrix Equations

Adding Matrices

Matrix Inverse

Matrices

Multiplying Matrices

Scalar Matrix Multiplication