Chapters
Matrices are fundamental tools in mathematics, used to organise numbers into rows and columns. Just as numbers can be classified into different types (like integers, fractions, or irrational numbers), matrices are classified based on their dimensions, the values of their elements, and their specific properties.
Understanding these types is essential for performing matrix operations like addition, multiplication, and finding inverses. Below, we explore the most common types of matrices.
Summary Table of Matrix Types
| Type | Description |
|---|---|
| Row Matrix | Has only one row. |
| Column Matrix | Has only one column. |
| Square Matrix | Has equal number of rows and columns. |
| Zero Matrix | All elements are zero. |
| Diagonal Matrix | All non-diagonal elements are zero. |
| Scalar Matrix | Diagonal elements are equal; others are zero. |
| Identity Matrix | Diagonal elements are 1; others are zero. |
| Upper Triangular | All elements below diagonal are zero. |
| Lower Triangular | All elements above diagonal are zero. |
| Symmetric Matrix | Matrix equals its transpose. |
| Antisymmetric Matrix | Matrix equals negative of its transpose. |
| Orthogonal Matrix | Product with transpose is Identity. |
| Singular Matrix | Has no inverse (Determinant is 0). |
| Regular Matrix | Has an inverse (Determinant is not 0). |
| Idempotent Matrix | Square equals itself. |
| Involutory Matrix | Square equals Identity. |
Classification by Dimensions
Row Matrix
A matrix is called a row matrix if it has exactly one row. The number of columns does not matter. It is essentially a horizontal list of numbers. An example of a row matrix:
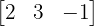
Column Matrix
A column matrix is the opposite of a row matrix. It has exactly one column, regardless of how many rows it contains. It appears as a vertical list. An example of a column matrix:
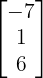
Rectangular Matrix
A rectangular matrix is the standard form where the number of rows (m) and the number of columns (n) are different. Its dimension is denoted as m x n. An example of a 2 x 3 rectangular matrix:
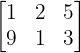
Square Matrix
If the number of rows equals the number of columns (m = n), the matrix is called a square matrix. In a square matrix, the elements where the row number equals the column number form the principal diagonal. An example of a 2 x 2 square matrix:
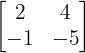
Classification by Elements
Zero Matrix
A zero matrix (often denoted by a bold 0) is a matrix where every single element is zero. It acts like the number 0 in standard arithmetic. A 2 x 2 zero matrix:
Diagonal Matrix
A diagonal matrix is a square matrix where all elements outside the principal diagonal are zero. The elements on the diagonal can be any number. An example:
Scalar Matrix
A scalar matrix is a specific type of diagonal matrix. It must meet two conditions:
- All non-diagonal elements are zero.
- All diagonal elements are equal to the same number (scalar). An example where the scalar is 2:
Identity Matrix
An identity matrix (usually denoted as I) is a unique diagonal matrix where every element on the principal diagonal is equal to 1, and all other elements are 0. A 3 x 3 identity matrix:
Triangular Matrices
- Upper Triangular Matrix: All elements below the principal diagonal are zero.
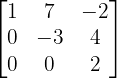
- Lower Triangular Matrix: All elements above the principal diagonal are zero.
Classification by Properties
Transpose Matrix
The transpose of a matrix is found by swapping its rows and columns. The first row becomes the first column, the second row becomes the second column, and so on.
If matrix A is:
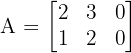
Then its transpose is:
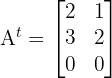
Symmetric Matrix
A square matrix is symmetric if it is identical to its own transpose. This means the matrix looks the same if you flip it over its diagonal.
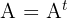
Antisymmetric (Skew-Symmetric) Matrix
A square matrix is antisymmetric if its transpose is equal to the negative of the original matrix.
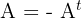
Regular vs. Singular Matrix
- Regular (Non-Singular) Matrix: A square matrix that has an inverse. Its determinant is non-zero.
- Singular Matrix: A square matrix that does not have an inverse. Its determinant is equal to zero.
Orthogonal Matrix
A matrix is orthogonal if multiplying the matrix by its transpose results in the Identity matrix.
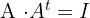
Idempotent and Involutory
- Idempotent: Multiplying the matrix by itself gives the original matrix:
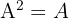
- Involutory: Multiplying the matrix by itself gives the Identity matrix (it is its own inverse):
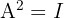
Practice Questions & Solutions
Identify the specific type of the following matrix. Be as specific as possible (e.g., if it is diagonal, check if it is also scalar or identity).
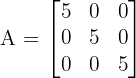
First, we check the dimensions. It is a 3 x 3 square matrix. Next, we look at the elements off the diagonal. They are all zero, so it is a diagonal matrix. Finally, we look at the elements on the principal diagonal. They are all equal to 5. Since the non-diagonal elements are zero and the diagonal elements are equal constants, it is a Scalar Matrix.
Answer: Scalar Matrix
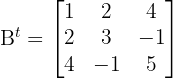
Given the matrix B below, calculate its transpose and state whether matrix B is symmetric.
To find the transpose, we switch the rows and columns. Row 1 (1, 2, 4) becomes Column 1. Row 2 (2, 3, -1) becomes Column 2. Row 3 (4, -1, 5) becomes Column 3. The transpose is:
Now we compare both matrices and we can see that:
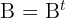
Answer: The transpose is identical to the original, so the matrix is Symmetric.
Determine if the matrix C is Involutory.
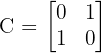
A matrix is involutory if its square equals the identity matrix:
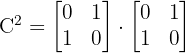
Perform row-by-column multiplication: Top-left: (0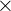 
0) + (1 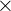1) = 1 Top-right: (0 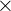1) + (1 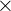0) = 0 Bottom-left: (1 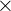0) + (0 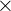1) = 0 Bottom-right: (1 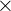1) + (0 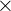0) = 1 The result is:
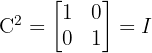
Answer: The matrix is Involutory.
Did you like this article? Rate it!
Loading...
I appreciate your work, thanks so much keep up the good work ✅
Hello Little P! Thanks very much for the positive feedback!
I didn’t get the same answer for the second question, ive also asked my friends and we all got the same answer it just didnt line up with yours. Apart from that, great website and thanks for the exercises.
Very nice and good explanation of matrix
Give some more examples of matrix
I want to more study about matrix that’s why I’m using Google