Chapters

Visual Interpretation of Correlation
Practice Problems and Solutions
Conclusion

Introduction

Humans are naturally wired to see patterns — we often link events, behaviours, or numbers and wonder if they’re connected.
In statistics, this idea is formalised through correlation, a measure that quantifies the strength and direction of a relationship between two variables.

For example, ice cream sales and shark attacks might both increase in summer, showing a positive correlation, but that doesn’t mean one causes the other.
This is a crucial lesson in statistics: correlation does not imply causation.

The correlation coefficient, usually represented by r, measures how strongly two variables are related.

Correlation Coefficient Formula

For two variables X and Y, the Pearson correlation coefficient is given by:

$\text{[math]}$

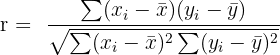
Where:

$\text{[math]}$ is the mean of the x-values
$\text{[math]}$ is the mean of the y-values
$\text{[math]}$ - ranges from -1 to +1

Interpretation:

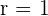$\text{[math]}$ : Perfect positive correlation
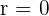$\text{[math]}$ : No correlation
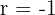$\text{[math]}$ : Perfect negative correlation

The best Maths tutors available

Visual Interpretation of Correlation

Graph Type	Correlation (r)	Description
A	1.0	Perfect positive correlation — as one variable increases, so does the other.
B	0.6	Moderate positive correlation — upward trend with some variation.
C	0.0	No correlation — no linear relationship between the variables.
D	-0.6	Moderate negative correlation — one increases as the other decreases.
E	-1.0	Perfect negative correlation — all points lie on a downward line.

Practice Problems and Solutions

Problem 1

Calculate and interpret the correlation coefficient for the following data:

Person	Hand Span (cm)	Height (cm)
A	17	150
B	15	154
C	19	169
D	17	172
E	21	175

Solution

Step 1: Calculate the means:

$\text{[math]}$

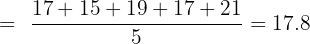
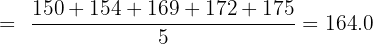
Step 2: Compute deviations and products:

Person	x−x̄	y−ȳ	product	(x−x̄)²	(y−ȳ)²
A	-0.8	-14.0	11.2	0.6	196.0
B	-2.8	-10.0	28.0	7.8	100.0
C	1.1	5.0	5.9	1.4	25.0
D	-0.8	8.0	-6.4	0.6	64.0
E	3.2	11.0	35.2	10.2	121.0

Totals:
Σ(x−x̄)(y−ȳ) = 74.0
Σ(x−x̄)² = 20.8
Σ(y−ȳ)² = 506.0

Step 3: Substitute into the formula:

$\text{[math]}$

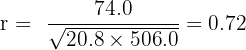
Interpretation:
There is a strong positive correlation between hand span and height. Taller individuals tend to have larger hand spans.

Problem 2

Calculate and interpret the correlation coefficient for the following data:

Person	Weight (kg)	Blood Pressure (mmHg)
A	150	125
B	169	130
C	175	160
D	180	169
E	200	150

Solution

Step 1: Calculate the means:

$\text{[math]}$

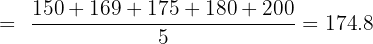
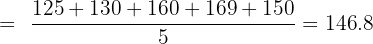
Step 2: Compute deviations and products:

Person	x−x̄	y−ȳ	Product	(x−x̄)²	(y−ȳ)²
A	-24.8	-21.8	540.6	615.0	475.2
B	-5.8	-16.8	97.4	33.6	282.2
C	0.2	13.2	2.6	0.0	174.2
D	5.2	22.2	115.4	27.0	492.8
E	25.2	3.2	80.6	635.0	10.2

Totals:
Σ(x−x̄)(y−ȳ) = 836.8
Σ(x−x̄)² = 1310.8
Σ(y−ȳ)² = 1434.8

Step 3: Substitute into the formula:

$\text{[math]}$

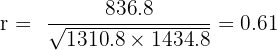
Interpretation:
There is a moderate positive correlation between weight and blood pressure — as weight increases, blood pressure tends to rise.

Problem 3

Calculate and interpret the correlation coefficient for the following data:

Person	Screen Time (hr)	Exam Score (%)
A	5	88
B	8	90
C	10	78
D	12	85
E	15	70

Solution

Step 1: Calculate the means:

$\text{[math]}$

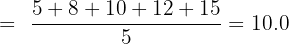
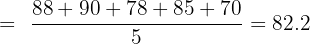
Step 2: Compute deviations and products:

Person	x−x̄	y−ȳ	Product	(x−x̄)²	(y−ȳ)²
A	-5.0	5.8	-29.0	25.0	33.6
B	-2.0	7.8	-15.6	4.0	60.8
C	0.0	-4.2	-0.0	0.0	17.6
D	2.0	2.8	5.6	4.0	7.8
E	5.0	-12.2	-61.0	25.0	148.8

Totals:
Σ(x−x̄)(y−ȳ) = -100.0
Σ(x−x̄)² = 58.0
Σ(y−ȳ)² = 268.8

Step 3: Substitute into the formula:

Interpretation:
There is a strong negative correlation between screen time and exam score: as screen time increases, exam scores tend to decrease.

Conclusion

Correlation helps us understand whether two variables move together — and how strongly.
A positive correlation means they rise together, a negative correlation means one rises while the other falls, and a zero correlation means no relationship at all.

This concept forms the basis of regression analysis, which allows us to make predictions using real data.

Summarise with AI:

Did you like this article? Rate it!

4.00 (18 rating(s))

Gianpiero Placidi

UK-based Chemistry graduate with a passion for education, providing clear explanations and thoughtful guidance to inspire student success.

Correlation Practice Problems and Solutions

Introduction

Correlation Coefficient Formula

Visual Interpretation of Correlation

Practice Problems and Solutions

Problem 1

Solution

Problem 2

Solution

Problem 3

Solution

Conclusion

Theory

Central Limit Theorem

Linear Correlation Coefficient

Type I and Type II Errors

Hypothesis Testing

Linear Regression

Sampling

Solution to Problem of Regression 4

Solution to Problem of Regression 5

Solution to Problem of Regression 6

Solution to Problem of Regression 8

Solution to Problem of Regression 3

Solution to Problem of Regression 5

Solution to Problem of Regression 6

Solution to Problem of Regression 9

Solution to Problem of Regression 2

Solution to Problem of Regression 3

Solution to Problem of Regression 2

Solution to Problem of Regression 8

Two Variable Statistics

Solution to Problem of Regression 1

Solution to Problem of Regression 7

Solution to Problem of Regression 1

Solution to Problem of Regression 4

Solution to Problem of Regression 7

Correlation

Covariance

One Tailed Test

Two Tailed Test

Exercises

Hypothesis Testing Problems

Problems of Regression

Correlation Problems and Solutions

Cancel reply