Chapters
The linear correlation coefficient is one of the fundamental concepts behind the interpretation of regression models. In order to understand the mathematics and ideas behind the correlation coefficient, try to solve the following problem by reviewing what you know. If you’re encountering this concept for the first time, read through this guide for a step-by-step walk through.
Problem 3
You are interested in knowing the relationship between the weather and tourism levels. To investigate, you collect data from the touristic centre in a city during one month in the summer, counting the number of people that arrive at the square at the same time every day. Given the data set below, what is the correlation between temperature and tourism? Interpret the correlation and name a few other reasons why these two variables are or are not related.
| Temperature | Number of Visitors |
| 12 | 87 |
| 21 | 150 |
| 20 | 110 |
| 25 | 90 |
| 17 | 85 |
| 15 | 70 |
| 13 | 90 |
What is the Correlation Coefficient?
The Pearson correlation coefficient, also known as the Pearson product-moment correlation coefficient, is one of the most powerful statistics in the field. Be careful not to confuse this with the coefficient of determination, which is also known as the “R squared” value. The correlation coefficient is a statistic that measures the strength of the linear relationship between two variables. A linear relationship between any two variables means that when the two variables are graphed, they follow a straight line. In other words, an increase or decrease in one variable will see a corresponding increase or decrease in the other variable as well. 
Derivation of Formula
The formula for the correlation coefficient is the following. [ rho_{xy} = frac{Cov(x,y)}{sigma_{x} sigma_{y}} ] While this formula may seem confusing at first, it is actually quite simple to understand when breaking down each element of the formula.
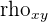 | Pearson product moment correlation |
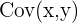 | Covariance between x and y |
 | Standard deviation of x |
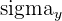 | Standard deviation of y |
Let’s take the first element, which is the covariance. The covariance of two variables measures the direction of the relationship between them. In other words, the covariance measures how two variables move together. Next, let’s look at the two elements of the denominator of the correlation coefficient. The standard deviation is a statistic that measures how far spread the variable is from the mean. The formulas for all three elements can be seen below.
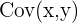| [ frac{sum_{i=1}^{n}(x_{i}- bar{x})(y_{i}- bar{y})}{n-1} ] |
| [ sqrt{frac{sum(x_{i} - bar{x}^2)}{n-1}} ] |
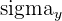| [ sqrt{frac{sum(y_{i} - bar{y}^2)}{n-1}} ] |
As you can see, these three elements are what go into deriving the correlation formula. In the numerator, you have the measure of the direction of the relationship between two variables. This relationship can be either positive or negative. If, for example, the relationship is positive, this means that a decrease in one variable would result in a decrease in another variable - and vice versa. On the other hand, a negative covariance would mean that a decrease in one variable would result in an increase in the other variable, and again vice versa. The denominator is the multiplication of the standard deviations of both variables. The standard deviation of a variable is a measure of dispersion. This means that it measures the spread of a variable around it’s mean. To derive the correlation coefficient formula, you first plug in the three elements of the formula into the correlation coefficient formula. [ frac{frac{sum_{i=1}^{n}(x_{i}- bar{x})(y_{i}- bar{y})}{n-1}}{sqrt{frac{sum(x_{i} - bar{x}^2)}{n-1}}*sqrt{frac{sum(y_{i} - bar{y}^2)}{n-1}}} ] Recall that in mathematics, the square root of a fraction is simply the square root of the numerator divided by the square root of the denominator. This means that the denominator becomes: [ frac{sum_{i=1}^{n}(x_{i}- bar{x})(y_{i}- bar{y})}{n-1} div ( frac{sqrt{sum(x_{i} - bar{x}^2)}}{sqrt{n-1}} * frac{sqrt{sum(y_{i} - bar{y}^2)}}{sqrt{n-1}} ) ] 
Cancelling out the denominator and the numerator, as they are both 
, and simplifying both the numerator and denominator, we get: [ frac{n sum xy - sum x sum y}{n} * frac{n}{sqrt{ (n sum x^2 - (sum x)^2) ( n sum y^2 - (sum y)^2) }} ] [ frac{n sum xy - sum x sum y}{sqrt{ (n sum x^2 - (sum x)^2) ( n sum y^2 - (sum y)^2) }} ]
Interpretation of Correlation Coefficient
The interpretation of the correlation coefficient is quite simple and can be summarized by the table below.
| Value | Direction | Strength | Interpretation |
| -1 | Negative | Very Strong | Perfect negative correlation |
| -0.3 | Negative | Weak | Very weak negative correlation |
| 0 | None | None | No correlation |
| 0.3 | Positive | Weak | Very weak positive correlation |
| 1 | Positive | Very strong | Perfect positive correlation |
Step by Step Solution
| Observation | Happiness Score | Work Hours |   |   |  |  |  |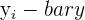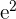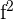
| 1.0 | 89.0 | 30.0 | 21.3 | -11.7 | -248.9 | 455.1 | 136.1 |
| 2.0 | 90.0 | 35.0 | 22.3 | -6.7 | -148.9 | 498.8 | 44.4 |
| 3.0 | 54.0 | 40.0 | -13.7 | -1.7 | 22.8 | 186.8 | 2.8 |
| 4.0 | 60.0 | 35.0 | -7.7 | -6.7 | 51.1 | 58.8 | 44.4 |
| 5.0 | 73.0 | 40.0 | 5.3 | -1.7 | -8.9 | 28.4 | 2.8 |
| 6.0 | 40.0 | 70.0 | -27.7 | 28.3 | -783.9 | 765.4 | 802.8 |
| Average | 67.7 | 41.7 | Total | -1116.7 | 1993.3 | 1033.3 |
Plugging this into the formula, we get: [ r_{xy} = frac{-1116.7}{sqrt{1993.3*1033.3}} = -0.78 ]
The platform that connects tutors and students
Did you like this article? Rate it!
Loading...
