Chapters

Regression Definition
Simple Linear Regression
Simple linear regression, or SLR, is a special type of regression. SLR involves only one independent and one dependent variable. Check out the breakdown of the SLR equation below.
| y | Response variable | The variable that is responsive to changes in the x variable |
| x | Explanatory variable | The variable that explains the variation in the y variable |
| Bo | Constant | The value of y if x were zero |
| B1 | Regression coefficient (slope) | The change in y if x increases by one unit |
A simple linear regression can help you understand the relationship between two variables. The table below summarizes the model’s estimate formulas.
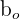 | 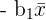 |
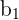 | 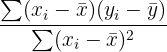 |
SLR Interpretation
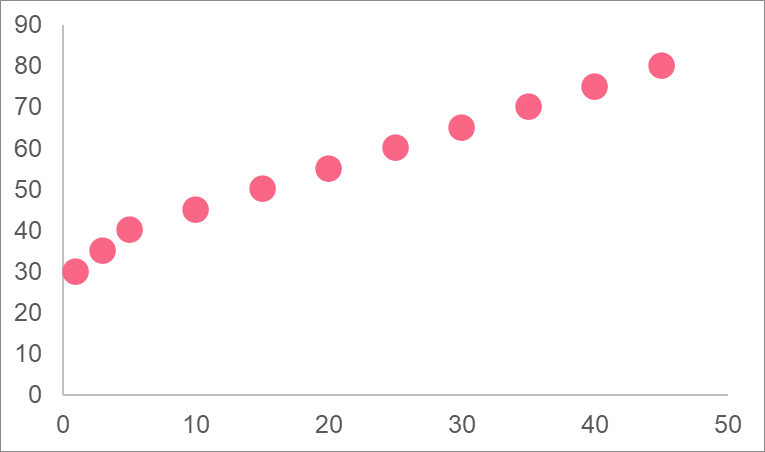
One of the most important components in a regression model is how you interpret its results. Take the graph from the previous example, where a regression line has been added.

There are several ways you can interpret this graph. There are a few intuitive remarks we can make before looking at the regression model, summarized below.
| Y | This variable has a small range compared to the x variable, it has a couple of extreme values |
| X | This variable has a large range compared to the y variable |
| Association | There appears to be a rather week relationship between the two variables |
Next, look at the equation for this regression model.

Recall that there are two elements we can interpret directly from this model: the constant and slope. On the other hand, we can also interpret the y and x variables if we plug in some numbers to the equation - also known as extrapolation and interpolation.
Multiple Linear Regression
Multiple linear regression, or MLR, is similar to SLR with the only difference being that in MLR, there is more than one explanatory variable included in the model. Because of these extra explanatory variables, the equation of the model looks slightly different. Take a look at the image below, which compares the SLR and MLR population and sample models.

Notice that there are more regression coefficients in the MLR model. Just like with SLR, MLR models are usually calculated using programs such as R or Python. However, you can also calculate MLR models by hand. Take a look at the image below for the equations for the regression coefficients for an MLR model with two explanatory variables.
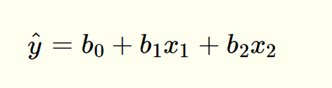
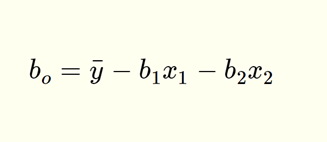
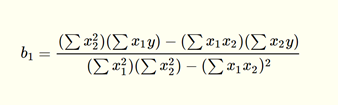
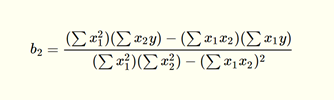
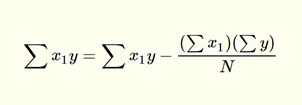
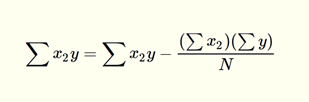

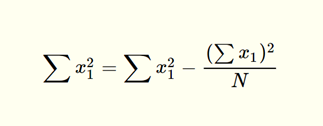
In order to understand these elements, take a look at the table below, which describes each of them in terms of what they mean.
| Element | Description |
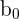 | The constant |
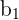 | The regression coefficient for the first explanatory variable (x1) |
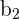 | The regression coefficient for the second explanatory variable (x2) |
 | The sum of all squared x1 values |
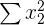 | The sum of all squared x2 values |
 | The sum of the all values of the first explanatory variable multiplied by the response variable |
 | The sum of the all values of the second explanatory variable multiplied by the response variable |
MLR Interpretation
In order to interpret a MLR model, you have to understand that the majority of the interpretation relies on the regression coefficients and the constant of the model. Take the following model as an example.
Y = 170 + 4.5x1 + 6.4x2
Here, the interpretation would be as follows.
| 170 | The constant, which is the value of y when x1 and x2 are zero |
| 4.5 | Y increases by 4.5 units when x1 increases by 1 unit, given that x2 is held constant |
| 6.4 | Y increases by 6.4 units when x2 increases by 1 unit, x1 held constant. |
Problem 1
Using the information above, calculate the MLR model. If you don’t recall the formulas, check the solution below.
| Element | Description |
 | 100 |
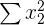 | 300 |
 | 250 |
 | 115 |
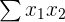 | 310 |
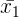 | 15 |
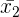 | 5 |
 | 25 |
Solution to Problem 1
To calculate the constant and regression coefficients, we need to plug in the data we have.
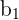 | 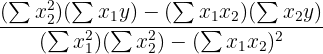 |
| \frac{(300*250) -(310*115)}{ (100*300) - (310^2)} = -0.59 |
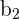 | 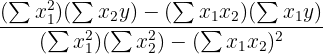 |
| \frac{(100*115) -(310*250)}{ (100*300) - (310^2)} = 0.79 |
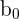 |  |
| 25 - (-0.59*15)-(0.79*5) = 30 |
Plugging this in to the final equation, we get:
\[
y = 30 - 0.59x_{1} + 0.70x_{2}
\]













Very Helpful. Thanks you guys for good job done to many
Thank you and I want to download these.
How is it?
Very nice and easy way.
Well explained.