Chapters

Descriptive v Inferential Statistics
Big data is something that everyone nowadays grows up knowing about. Whether you’re logging into your favourite social media app or looking into new mini-fridges, you’ll have noticed that many companies use your personal information to try and sell you their products.
One American retail corporation did exactly that in one now infamous of leveraging personal information to sell things. Using statistics, it used information on expecting mothers to send coupons to women who exhibited similar shopping patterns. They ended up predicting the pregnancy of a young woman before even her father knew about it.
This case can help you understand the major difference between descriptive and inferential statistics. Descriptive statistics can be used to investigate, analyse and display information about observations within a dataset. Inferential statistics, on the other hand, uses the information about the observations within a dataset to try and predict characteristics for observations outside the dataset.
Inferential statistics methods can be found in many different statistical applications including regression, social network and machine learning analysis. There are two different frameworks that can be used to apply inferential statistics: Bayesian and Frequentist statistics. While there are arguments in defence and in critique of both, they both use probability for prediction power. Here, we’ll cover Bayesian statistics.
Probability Theory
Because the basis of inferential statistics relies on probabilities, it is extremely important to get a clear understanding of the fundamental concepts that tie mathematics and statistics together. Probability Theory is a branch of mathematics that deals with all the characteristics and concepts of probability.
There are a couple of definitions and concepts in probability theory that you should understand before delving into the Central Limit Theorem. The first is a random variable, which is a variable whose value is random and unknown. It can be helpful to think of random variables as random outcomes, which can be anything from the classic example of a coin flip to a more subtle example like the amount of rain on any given day.
Random variables, which we’ll call RVs from now on, are usually denoted by a capital letter, like X. RVs can be either discrete or continuous. Discrete RVs are those that take on a distinct, finite set of numbers. Continuous RVs, on the other hand, can take on an infinite set of numbers within an interval. For example, while a coin toss is discrete (heads or tails), rain is continuous (583mm, 583.1mm, 583.11mm, etc.).
The number of each possible outcome for discrete and continuous RVs can be presented in a probability distribution. A probability distribution, like the one below, maps out the probability of each possible value of an RV.

Central Limit Theorem Definition
To understand the CLT, let’s start with a non-normal distribution of a population, whose mean is 166.4 cm and standard deviation is 14.2 cm. This population distribution is depicted below.
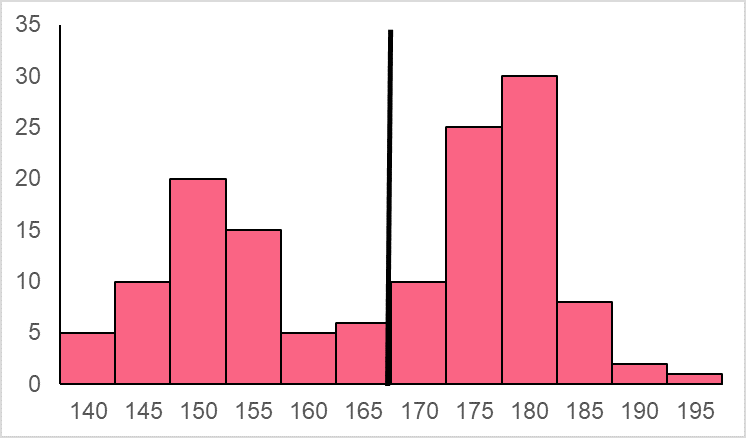
Above, you can see one of the most common non-normal distributions, known as a bi-modal distribution because it has two distinct modes. Other common non-normal distributions are left and right skewed distributions.
Say that this bi-modal distribution represents the heights of adult males and females. We take a sample from this population whose sample size, n, is equal to 50. That simply means that you take a sample of 50 people’s heights within your population. From those 50 people, we get a sample distribution like the one below.

This sample has a mean height of 168.6 cm, which is the sample mean. However, if we were to take another sample of 50 people’s heights from the same population, we’re bound to get a different combination of heights, which will result in another sample distribution, like the one below.
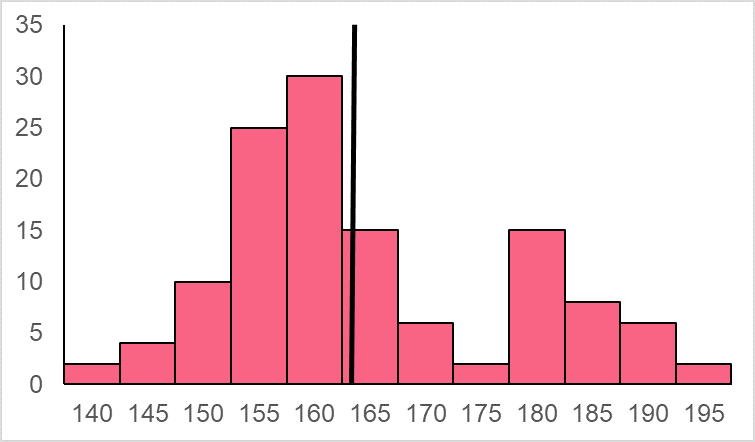
This time the sample mean height is 164.7 cm. Let's imagine that we spend all day taking samples of 50 people from a population, each time measuring the mean height of that sample. At the end of the day, if we managed to take 70 different samples, we would end up with 70 different sample means. If we were to plot these 70 different samples, we would end up with something the distribution below.
This distribution is known as a sampling distribution. Notice the difference between a sample distribution and sampling distribution. In this example, our sample distribution shows us the distribution of our observations of different heights for our sample. Conversely, our sampling distribution shows us the distribution of the means of all of those samples.
This is why the sampling distribution is defined as the probability distribution of a statistic, or a sample measure, observed from a large number of samples. The Law of Large Numbers, or LLN, tells us that a large enough sample will give us a sample mean that approximates or equals the true population mean, which we can observe from the distribution.
Notice as well that the sampling distribution follows a normal distribution. This is what the Central Limit Theorem, or CLT, is about and why it’s one of the most powerful concepts of probability theory. It states that the sampling distribution of the mean of any independent, random variable will be normal or approximately normal if the sample size is large enough.
Formally, the sampling distribution is centred at the true population mean (which we get from the LLN) and has a standard deviation of the true mean divided by the square root of the sample size.
The notation for this sampling distribution is the following:

As you can see from the standard deviation formula, the higher the sample size, the smaller the standard deviation. Take a look at the table below to differentiate between the formulas for the sample distribution and sampling distribution.
| Sample Mean | [ bar{x} = frac{x_1 + x_2+...x_n}{n} ] |
| Sample SD | [ sigma = frac{sum(x_{i}-bar{x})}{n-1} ] |
| Sampling Distribution Mean | [ bar{x} = mu ] |
| Sampling Distribution SD | [ sigma_{bar{x}} = frac{sigma}{sqrt{n}} ] |
Step-by-Step Example of CLT
To best illustrate the power of the CLT, let’s start off with a uniform population distribution.
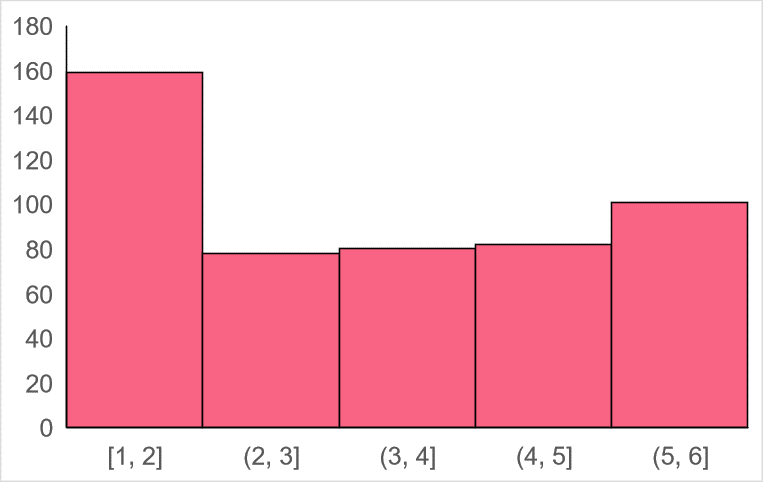
Let’s say that this distribution represents the number on the faces from die rolls. As you can see, the numbers on the bottom represent the possible set of outcomes, which is rolling any number from 1 to 6. This is a classic example of an independent, random variable because of the fact that the outcome of one roll of a die does not depend on the previous roll and the outcomes of all rolls are random.
Let’s say that this particular brand of die has a population mean of 3.5 and standard deviation of 1.71. We start by rolling the dice 10 times and record the outcomes, giving us a sample size of 10. We repeat this 500 times and get the following distribution with a mean of 3.53 and a standard deviation of 0.54.
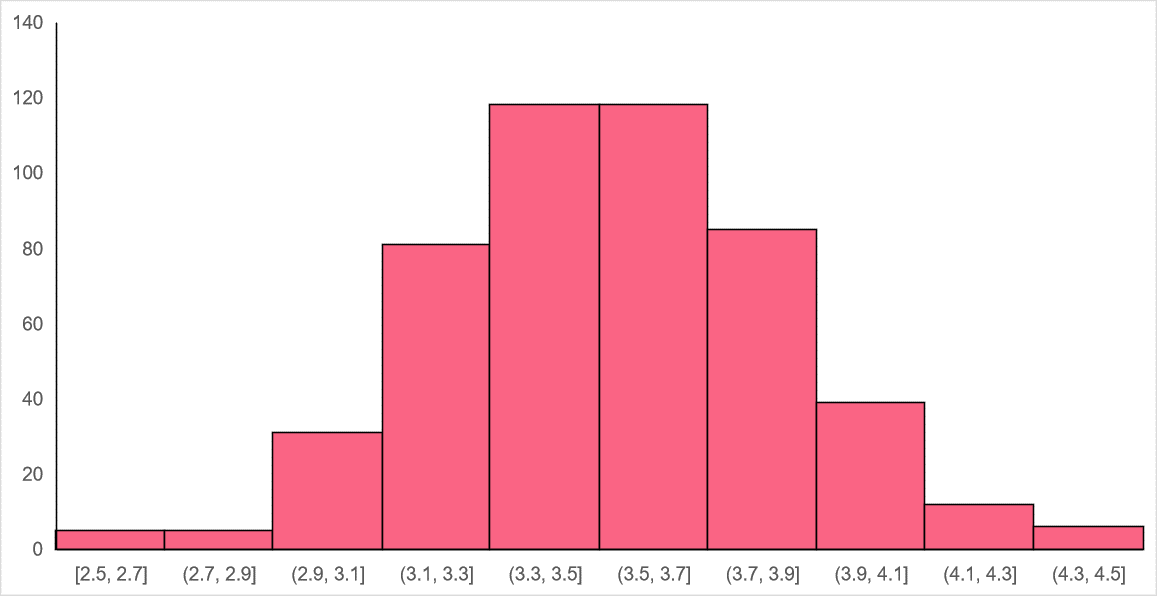
As we can see, while the distribution is approximately normal and the mean of the sampling distribution approaches the population mean, it is not as precise as we can get. This is why the rule of thumb for the CLT is to use a sample size of at least 30 and above. Increasing our sample size to 30 and running our experiment 500 times again, we get the following distribution with a mean of 3.5 and a standard deviation of 0.32.
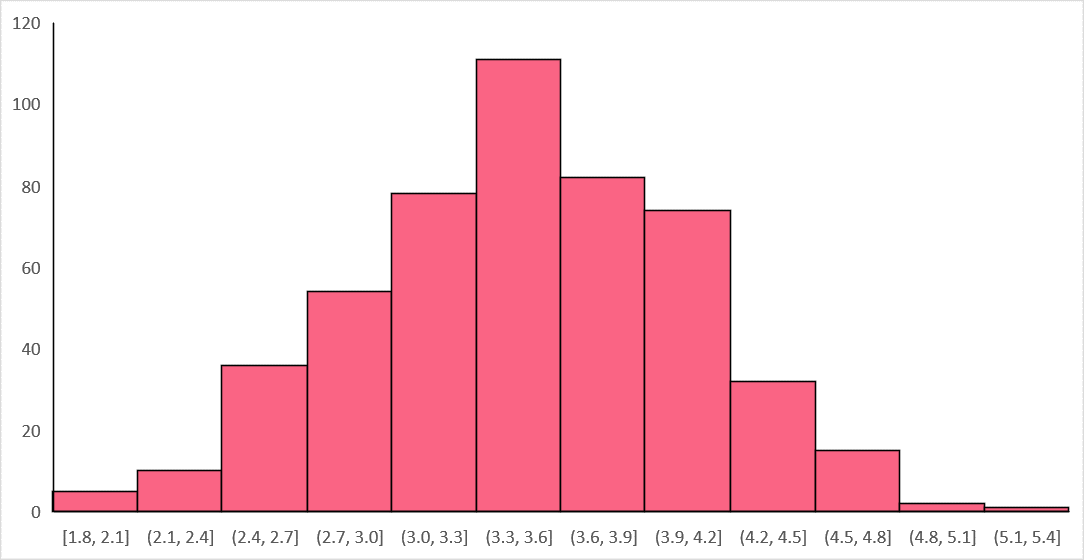
The bigger our sample size is, the closer we are to the true population parameter and the lower our standard deviation. Take a look at the table below to see how the sampling distribution’s standard deviation changes as the samples size increases.
The mean and standard deviation around found in the table below.
| Sampling distribution SD | |
| n = 10 | 0.54 |
| n = 30 | 0.32 |
| n = 100 | 0.17 |
| n = 1000 | 0.054 |
The main takeaway from the CLT is that it can be a pretty powerful tool for hypothesis testing. If you have a variable whose distribution is non-normal, you can use the sampling distribution of the mean in order to take advantage of the properties of normal distributions.













Very Helpful. Thanks you guys for good job done to many
Thank you and I want to download these.
How is it?
Very nice and easy way.
Well explained.