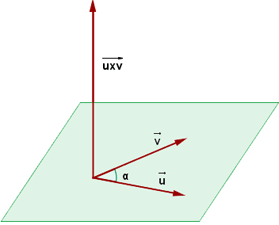
Vectors can be multiplied by each other but it isn't as simple as you think. There are two types of multiplication in vectors. One is the dot product which is also known as scalar product and another one is the cross product. The cross product of two vectors is another perpendicular vector to the two vectors. The direction of the resultant vector can be determined by the right-hand rule. The thumb (u) and index finger (v) held perpendicularly to one another represent the vectors and the middle finger held perpendicularly to the index and thumb indicates the direction of the cross vector.
There are some points that you need to remember when using the cross product. The first point is that  is a vector and the second point is that
is a vector and the second point is that 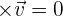 if both vectors (
if both vectors ( and
and  ) are parallel or in opposite direction. However, if both vectors are perpendicular then the
) are parallel or in opposite direction. However, if both vectors are perpendicular then the  will be equal to the product of their magnitudes. This all happens because of the
will be equal to the product of their magnitudes. This all happens because of the 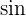 ratio because
ratio because  is the product of magnitudes of both vectors and
is the product of magnitudes of both vectors and 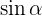
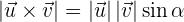
The cross product can be expressed by the determinant:
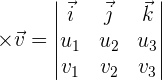

Calculate the cross product of the vectors 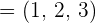 and
and  .
.
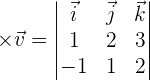
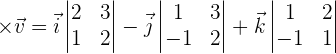

Find the cross product of the vectors  and
and  and check that the resultant vector is orthogonal to
and check that the resultant vector is orthogonal to  and
and  .
.

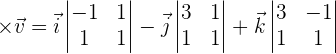


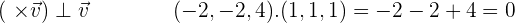
The cross product of  is orthogonal to the vectors
is orthogonal to the vectors  and
and  .
.
Find various Maths tutors near me on Superprof.

Area of a Parallelogram
Geometrically, the magnitude of the cross product of two vectors coincides with the area of the parallelogram whose sides are formed by those vectors. We all know that area of the parallelogram is equal to  . Let's solve for h:
. Let's solve for h:
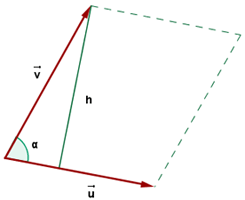

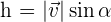
Plugging the value of h in the area of parallelogram equation:

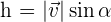
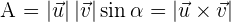
Example
Find the area of the parallelogram which is formed by the vectors  and
and 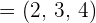
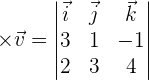
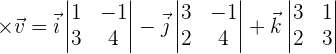

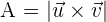

Area of a Triangle
There are many methods to find the area of a triangle, however, finding the area with the help of vectors? That is possible as well. To understand this, you need to be familiar with 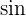 law.
law.
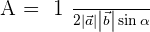
Since we know that 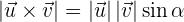 , hence:
, hence:
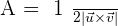

Example
Determine the area of the triangle whose vertices are the points 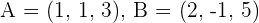 and
and 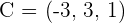 .
.


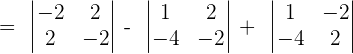
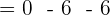
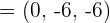
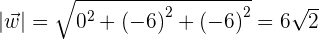

Cross Product Properties
1. Anticommutative.
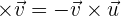
2. Compatible with scalar multiplication.

3. Distributive over addition.

4. The cross product of two parallel vectors is equal to the zero vector.

5. The cross product 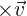 is perpendicular to
is perpendicular to  and
and  .
.













