Chapters
Food usually come in can packing. Ever wonder what kind of shape is the can? Mathematicians named it the cylinder. The question is what is a cylinder? Let's talk about it.

What is a Cylinder?
A cylinder is a three-dimensional shape that has identical circles at the top and bottom. Basically, it is the derivative of a circle that is drawn in all three dimensions. If the circle gets height then it will be transformed into a cylinder. Consider the below diagram.
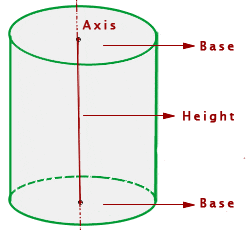
That is a cylinder. It has some parts. To understand the cylinder perfectly, you need to understand all the parts of the cylinder.
Axis
The axis is the fixed side about which the circle turns.
Bases
The bases are the two circles that generate the sides perpendicular to the axis.
Height
The height is the distance between the two bases.
Unfold of a Cylinder
To investigate the cylinder more, we need to unfold its secrets by unfolding it. Without any delay, let's open this object.

To be honest, the unfolding figure of the cylinder looks like a divide sign, right? The above picture could be used to find the lateral area as well as surface area.
Lateral Area of a Cylinder
The lateral area is the area of the cylinder excluding the top and bottom of the cylinder. With the help of the unfolded area, the lateral area of the cylinder is:

Surface Area of a Cylinder
The surface area is the sum of areas that covers the surface of the geometry. The surface area of a cylinder is:
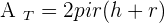
Volume of a Cylinder
The volume of a cylinder means the total space occupied by the cylinder. This covers the space occupied by the boundary as well as the space inside of that cylinder. Use the below formula to calculate the volume of the cylinder:
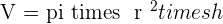
Examples
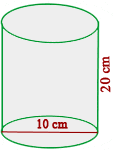
Calculate the quantity of sheet metal that would be needed to make 10 cylindrical canisters with a diameter of 10 cm and a height of 20 cm.
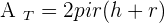

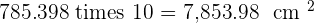
The height of a cylinder is the same length as the circumference of its base. Its measured height is 125.66 cm. Calculate the surface area and volume of the cylinder.
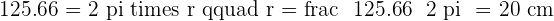
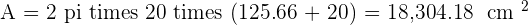

Four cubes of ice with an edge of 4 cm each are left to melt in a cylindrical glass with a radius of 6 cm. How high will the water rise when they have melted?
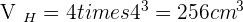

A cylindrical container with a radius of 5 cm and a height of 10 cm is filled with water. If the total mass of the filled container is 2 kg, what is the mass of the empty container?
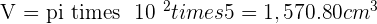
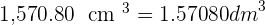
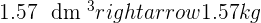
mass of the container = 













What is frac and sqrt
Interested learning more