Are you looking for formulas for the calculation of the volume of different polyhedrons? Then you came to the right place! In this resource, we made a list of formulas for volume for different polyhedrons. A handful of formulas will help you increase your productivity.
The volume of a tetrahedron is the product of the cube of the edge of the tetrahedron and the ratio of the square root of 2 and twelve and the cube of the edge of the tetrahedron.
Octahedron
The volume of an octahedron is the product of the cube of the edge of the octahedron and the ratio of the square root of two and 3.

or

The above formula is for an icosahedron that contains 20 faces. The variable "a" denotes the edge of a icosahedron.
The above formula is the formula for volume of a dodecahedron that contains twelve faces. All you need is the length of an edge of dodecahedron to find the volume.
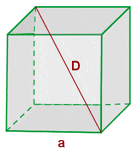
The volume of a cube is equal to the cube of an edge of a cube.
Cuboid
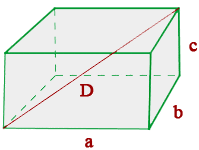
The volume of a cuboid is the product of all three dimensions of a cuboid.
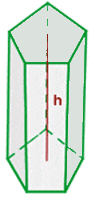
Prism
The volume of the prism is equal to the product of the base area and height between the top and the bottom of the base.

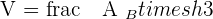
To find the volume of a pyramid, you need the base area and the height from the base to the top point. Once you have the information, multiply the base area with the height and then divide the total value by 3.

A = Area of the larger base
A' = Area of the smaller base

To find the area of a truncated pyramid, you need the height between both bases as well as the area of both bases. Use the above formula to calculate the volume of a truncated pyramid.
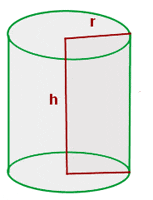
The volume of the cylinder is the product of two pi, the square of the radius, and the height of the cylinder.
Cone

To find the volume of a cone, multiply the value of pi with the square of the base radius of the cone and the height of the cone. Then divide the total value by three and the final value will be the volume of a cone.
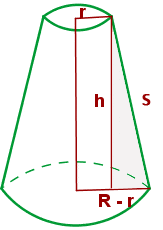
Truncated Cone
To find the volume of a truncated cone, you need the radius of the top and bottom base. Furthermore, you will also require the height of the cone. Once you have all the information available, use the above formula to calculate the volume of a truncated cone.
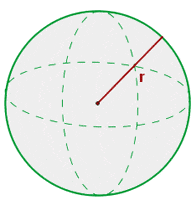
Sphere is a spherical object whose volume is equal to the product of four-third, value of pi, and the cube of the sphere's radius.
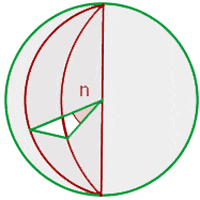
A spherical wedge is a part of a sphere. To find the volume of a spherical wedge, you need the radius of the sphere and the central angle. Once you have both of them, use the above formula to get the volume of the spherical wedge.
Spherical Cap
Like a spherical wedge, a spherical cap is also a part of a sphere. The above formulas are for the calculation of the radius of the sphere and the volume of the spherical cap. To find the volume of the spherical cap, you will require the radius of the sphere and the height. To find the radius of the sphere, the formula is already given. Use the formula to find the radius of the sphere and then use the volume formula to calculate the volume of a spherical cap.
Spherical Segment
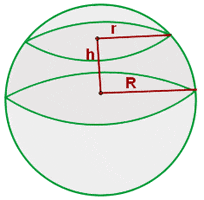
Spherical segment is another special part of a sphere. The above formula is used for the calculation of the volume of a spherical segment.
Did you like this article?
Rate it!

Loading...
Emma
I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.





 or
or 

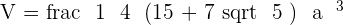


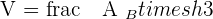


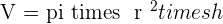


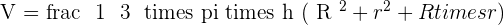



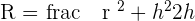

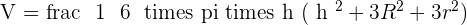





What is frac and sqrt
Interested learning more