Chapters
You might have heard about the pentagon, the hexagon, and other polygons too. Some of you might have heard about polyhedrons too and then there are icosahedrons. The name of this figure might be giving you sweats but, at SuperProf, we make things simple and easy for students. In this article, we will explain to you about regular icosahedron.

What is an Icosahedron?
An Icosahedron is a three-dimensional shape that contains 20 faces. It belongs to the family of polyhedrons, why? Because of the three-dimensional shape and after all, it is a polygon. Consider the below image.
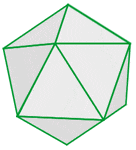
You might have seen this shape in board games. Usually, dies come in this shape for different board games. We want you to focus on a single face. Does the face look familiar? Something like a triangle, right? Absolutely! The face of the icosahedron is a triangle. That also means that icosahedron is made up of triangles. As mentioned before, an icosahedron contains 20 faces and since the face is a triangle, we can conclude that the icosahedron is a polyhedron that is composed of 20 triangles
What is a Regular Icosahedron?
Whenever you hear the word, "regular" before a polygon or polyhedrons, it means that the shape contains uniform dimensions. Hence, a regular icosahedron belongs to the family of the regular polyhedron which means every triangle is an equilateral triangle. Hence, all the lengths and angles of the triangles will be the same. On the other hand, a simple icosahedron can non-uniform triangles. If a polyhedron contains 20 triangles as its faces then it is an icosahedron but if the polyhedron contains 20 equilateral triangles as its faces then it is a regular icosahedron, that is the difference between an icosahedron and a regular icosahedron.
Unfold of a Regular Icosahedron
Unfolding 3-dimensional shapes is pretty fun. You always get something which is interested and satisfying to view. The more complex the shape is the more satisfying the unfolding of that shape. Without any further ado, let's unfold the regular icosahedron.
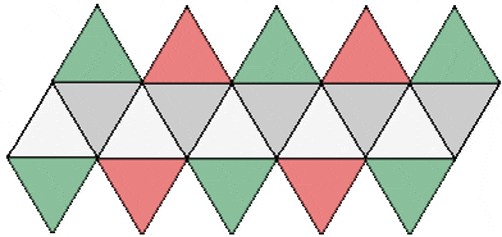
The above image is the unfolded icosahedron. Does it look satisfying to you? If you look carefully, there is a pattern. There is a repetition of four triangles that are joined together on an inclined plane. However, one thing is clear and that is icosahedron is all about triangles that are merged together to form a complex geometry.
Characteristics of an Icosahedron
The unfolding of the regular icosahedron is not only satisfying but also helped us to analyze this shape. Below are the characteristics of an icosahedron:
Number of faces: 20.
Number of vertices: 12.
Number of edges: 30.
Number of concurrent edges at a vertex: 5.
Surface Area of a Regular Icosahedron
Of course, this isn't geometry if it doesn't involve volumes and area. This area isn't a simple area, when we are working in a three-dimension, we calculate the surface area of the figure. Surface area means the total space occupied by the surface of an object. Below is the formula for finding the surface area of a regular icosahedron:

Volume of a Regular Icosahedron
When you were working with geometrical figures in two-dimension, the area was pretty common but you rarely encounter volume. This is because, in 2-dimension, we don't consider the height and the height is the third dimension. Finding volume of figures is very common in three-dimensional shapes.

Example
Calculate the surface area and volume of a regular icosahedron with an edge of 5 cm.

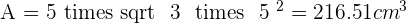















What is frac and sqrt
Interested learning more