Chapters

Circle Definition

| A | B |
| Pyramid | Can be broken down into four triangles and a square |
The base of a cone is simply a circle. Let’s take a look at the characteristics that define circles.

| A | The radius goes from the centre point to the edge of the circle. |
| B | The diameter goes from end to end of the circle, passing through the centre point. |
| C | The circumference is the length around the circle, or the perimeter |
Let’s take a look at the formula for the area of any circle.
| Formula | |
| Area | 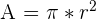 |
Cylinder
Now that you know the properties of a circle, let’s take a look at what a cylinder is. A cylinder is an easier three dimensional shape to understand than a cone. This is because it can be broken down into simple shapes.
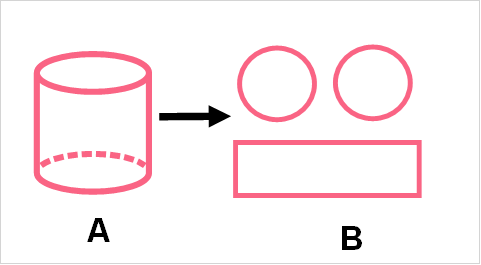
| A | B |
| Cylinder | Can be broken down into a rectangle and a circle |
As you can see, a cylinder is nothing more than a base of a circle and a body of a rectangle. We can easily find the area of these two shapes. When we add up the area of these two, we get a special type of area called a surface area.
| Definition | When it’s used | |
| Surface Area | The area of the ‘surface’ of the shapes that make up a three dimensional object | For three dimensional shapes |
Surface Area of a Cylinder
In order to find the surface area of a cylinder, we simply need to take the sum of the area of the circle at its base and the rectangle that forms its body. Let’s recall the formula for the area of a rectangle.
| Rectangle | A = l*w |
| Rectangle of a cylinder | A = l*h |
When you have the rectangle of a cylinder, the width of the cylinder is simply the height of the cylinder.

| Rectangle | A = l*w |
| Rectangle of a cylinder | A = C*w |
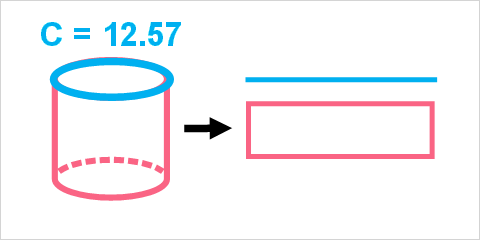
| Rectangle Area | Area of Two Circles | Surface Area |
| C*h = | 2C = | 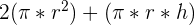 |
Cone Definition
Now, let’s take a look at a cone. A cone is a three dimensional shape that also has a base of a circle. However, instead of having the body of a rectangle, it has the body of an ice cream cone.
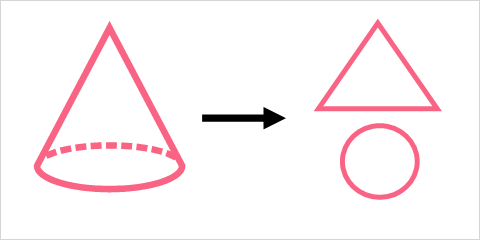
| A | B |
| Cone | Can be broken down into a circle and a ice cream cone shape |
While it might seem like an unusual shape, we encounter cones in daily life all the time. A cone has what is called a base, which is the bottom, and an apex, which is the top point of the cone.
Surface Area of a Cone
The surface area of a cone can be found with the following formula.
| Formula | |
| Cone Surface Area | 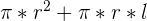 |
Let’s take a look at what these mean.

| l | The length of the slant height of the cone |
| r | The radius of the circle |
| h | The height from the centre point of the circle to the apex |
We get the surface area by simply adding the area of the circle to the area of the cone shape.
Lateral Area of a Cone
In order to understand what the lateral area is, you should first know what it is. The lateral area of the cone is simply the part of the cone that is shaped like a cone or triangle.

| A | Lateral Area | A = 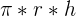 |
| B | Circle Area | A = 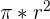 |
The lateral area is simply pi times the radius and height.
Volume of a Cone
The volume of a cone can be found with the following formula.
| Formula | |
| Cone Volume | 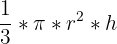 |
As you can see, the volume of the cone is simply ⅓ times the lateral area of the cone. The volume of any shape is the quantity that a three dimensional shape can hold. While the surface area is simply the total area on the surface of an object, the volume is all the space inside of the object.
Truncated Cone
In order to understand what a truncated cone is, you should know the definition of truncate, or truncated.
| Definition | |
| Truncated | To truncate is to shorten. If something is truncated, it means that it has been shortened or cut. |
| Truncated Cone | A cone that is cut by a plane parallel to its base. |

| A | B |
| Truncated Cone | Can be broken down into two circles and a ice cream cone shape |
Formulas for a Truncated Cone
In order to find the volume and surface areas of a truncated cone, we simply need to follow the formulas below.
| Truncated Cone | Formula |
| Lateral Area | 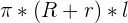 |
| Surface Area |  |
| Volume | 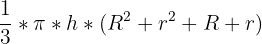 |
Keep in mind that R is the radius of the bigger circle and r is the radius of the smaller one.













What is frac and sqrt
Interested learning more