Chapters
Cuboids, cylinders, tetrahedrons, pyramids, we all have gone through them but the list of polyhedrons doesn't end here. In fact, we are going to talk about an uncommon polyhedron that you might have never heard before. We made a separate resource for this polyhedron and the name of this polyhedron is the Dodecahedron.

What is a Dodecahedron?
If you are looking for the textbook definition then it is a polyhedron that contains twelve faces. The word, dodecahedron, can be split into two words, "dodeca" and "hedron". The origin of both words is from ancient Greek, dodeca is a prefix that means twelve and hedron means faces. Let's focus on one of its faces. We have an image of a dodecahedron for you, consider the below image.
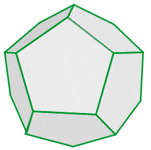
Guess which shape is the face is? Yes, it is a pentagon. Let's update our definition, dodecahedron is a polyhedron that contains 12 pentagons. You must be wondering what is a regular dodecahedron? Keep on reading to find it out.
Regular Dodecahedron
One thing is for sure and that is the shape will be a polyhedron that contains twelve pentagons. The only difference between regular dodecahedron and dodecahedron is that the regular dodecahedron contains twelve equally sized regular pentagons. In simple words, a regular dodecahedron is a regular polyhedron composed of twelve equally sized regular pentagons.
Unfold of a Regular Dodecahedron
You can convert a three-dimensional object into a two-dimensional object by unfolding it. This unfolding of a three-dimensional figure helps in understanding this geometry even further. We can use the unfolded geometry to learn about its characteristics as well as we can come up with a formula that will allow us to find the surface area of this geometry. Below is the image of an unfolded dodecahedron.
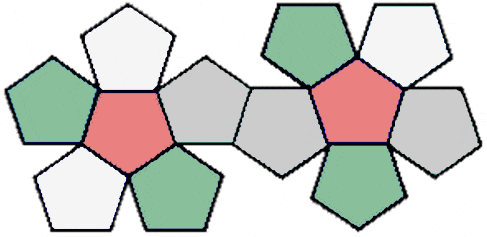
Characteristics of a Dodecahedron
To understand more about dodecahedron, we need to take a look at its characteristics. The characteristics of every polyhedron are different and that makes it special as well as interesting. Below are some main characteristics of the dodecahedron.
Number of faces: 12.
Number of vertices: 20.
Number of edges: 30.
Number of concurrent edges at a vertex: 3.
Surface Area of a Regular Dodecahedron
Surface area means the total space occupied by the boundary of the shape. In this case, we are talking about the boundary of the dodecahedron. Finding surface area can be troublesome, however, at SuperProf, we make things easy. You can use the below formula to calculate the surface area of a regular dodecahedron. All you will need is the apothem and the edge of a dodecahedron and plug it in the below equation and get the surface area.
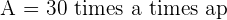
Volume of a Regular Dodecahedron
Volume means the total space of geometry. Therefore, the volume of a regular dodecahedron is the total space occupied by a regular dodecahedron. Finding the volume of a regular dodecahedron is very easy. All you need is the measurement of any side (since all sides are equal in length). Below is the formula for finding the volume of a regular dodecahedron:
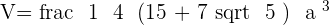
Example
Calculate the surface area and volume of a regular dodecahedron with an edge of 10 cm, knowing that the apothem of one side measures 6.88 cm.















What is frac and sqrt
Interested learning more