Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Exercise 18
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12
- Solution of exercise 13
- Solution of exercise 14
- Solution of exercise 15
- Solution of exercise 16
- Solution of exercise 17
- Solution of exercise 18

Exercise 1
Calculate the surface area and the volume of a regular tetrahedron with an edge of 5 cm.
Exercise 2
Calculate the diagonal, lateral area, surface area and volume of a cube with an edge of 5 cm.
Exercise 3
Calculate the surface area and the volume of a regular octahedron with an edge of 5 cm.
Exercise 4
Calculate the surface area and volume of a dodecahedron with an edge of 10 cm, knowing that the apothem of one face measures 6.88 cm.
Exercise 5
Calculate the surface area and the volume of a regular icosahedron with an edge of 5 cm.
Exercise 6
Calculate the lateral area, surface area and volume of a prism whose base is a rhombus with diagonals of 12 and 18 cm in length.
Exercise 7
Calculate the lateral area, surface area and volume of a square pyramid whose base edge is 10 cm and its height is 12 cm.
Exercise 8
Calculate the lateral area, surface area and volume of a hexagonal pyramid with a base edge of 16 cm and a side edge of 28 cm.
Exercise 9
Calculate the lateral area, surface area and volume of a truncated square pyramid whose base edges are 24 and 14 cm and whose lateral edge is 13 cm.
Exercise 10
Calculate the lateral area, surface area and volume of a cone whose slant height is 13 cm and base radius is 5 cm.
Exercise 11
Calculate the lateral area, surface area and volume of a cone whose height is 4 cm and base radius is 3 cm.
Exercise 12
Calculate the lateral area, surface area and volume of a truncated cone with radii of 2 and 6 cm and a height of 10 cm.
Exercise 13
Calculate the lateral area, surface area and volume of a truncated cone with radii of 12 and 10 cm and a slant height of 15 cm.
Exercise 14
Calculate the area of the circle resulting from cutting a sphere with a 35 cm radius by a plane whose distance from the centre of the sphere is 21 cm.
Exercise 15
Calculate the area and volume of a sphere inscribed in a cylinder with a height of 2 m.
Exercise 16
Calculate the volume of a hemisphere with a radius of 10 cm.
Exercise 17
Calculate the area and volume of the following spherical cap.
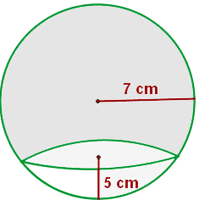
Exercise 18
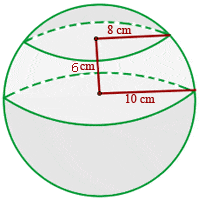
Calculate the area of the spherical zone and the volume of a spherical segment whose radius circles are 10 and 8 cm and the distance between them is 6 cm.
Solution of exercise 1
Calculate the surface area and the volume of a regular tetrahedron with an edge of 5 cm.
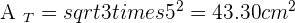
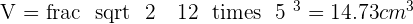
Solution of exercise 2
Calculate the diagonal, lateral area, surface area and volume of a cube with an edge of 5 cm.
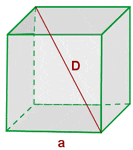

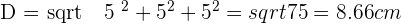
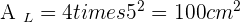
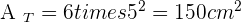

Solution of exercise 3
Calculate the surface area and the volume of a regular octahedron with an edge of 5 cm.
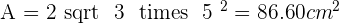
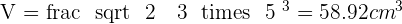
Solution of exercise 4
Calculate the surface area and volume of a dodecahedron with an edge of 10 cm, knowing that the apothem of one face measures 6.88 cm.


Solution of exercise 5
Calculate the surface area and the volume of a regular icosahedron with an edge of 5 cm.
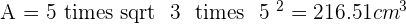

Solution of exercise 6
Calculate the lateral area, surface area and volume of a prism whose base is a rhombus with diagonals of 12 and 18 cm in length.
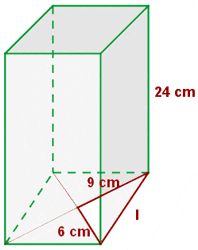
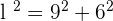
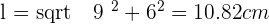
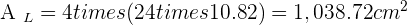
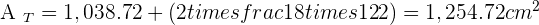
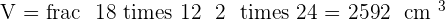
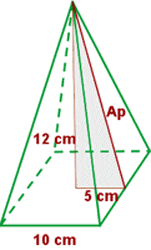
Solution of exercise 7
Calculate the lateral area, surface area and volume of a square pyramid whose base edge is 10 cm and its height is 12 cm.
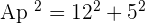
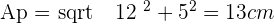
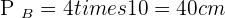
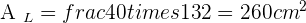


Solution of exercise 8
Calculate the lateral area, surface area and volume of a hexagonal pyramid with a base edge of 16 cm and a side edge of 28 cm.
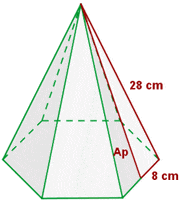
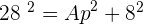

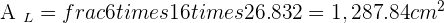
Solution of exercise 9
Calculate the lateral area, surface area and volume of a truncated square pyramid whose base edges are 24 and 14 cm and whose lateral edge is 13 cm.
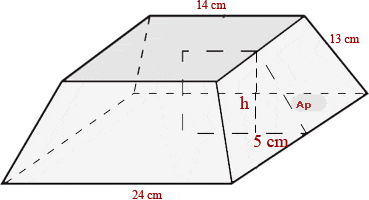
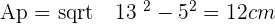
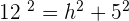
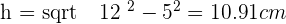
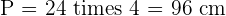
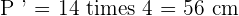

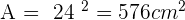
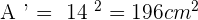
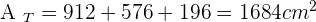

Solution of exercise 10
Calculate the lateral area, surface area and volume of a cone whose slant height is 13 cm and base radius is 5 cm.
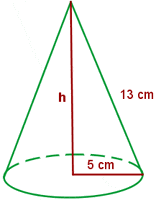
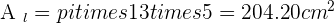
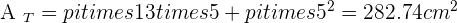
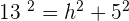


Solution of exercise 11
Calculate the lateral area, surface area and volume of a cone whose height is 4 cm and base radius is 3 cm.
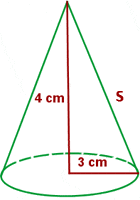
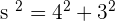
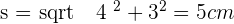
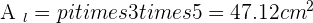
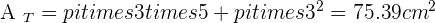
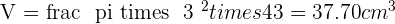
Solution of exercise 12
Calculate the lateral area, surface area and volume of a truncated cone with radii of 2 and 6 cm and a height of 10 cm.
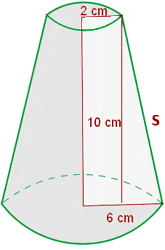
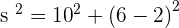
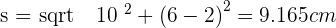
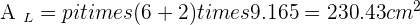
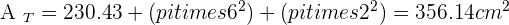
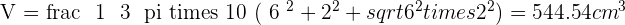
Solution of exercise 13
Calculate the lateral area, surface area and volume of a truncated cone with radii of 12 and 10 cm and a slant height of 15 cm.

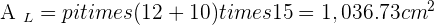
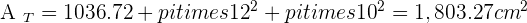
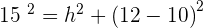
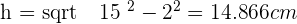
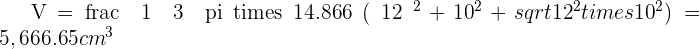
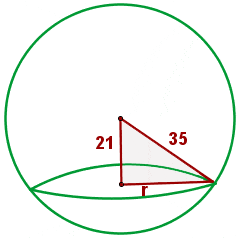
Solution of exercise 14
Calculate the area of the circle resulting from cutting a sphere with a 35 cm radius by a plane whose distance from the centre of the sphere is 21 cm.

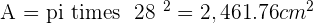
Solution of exercise 15
Calculate the area and volume of a sphere inscribed in a cylinder with a height of 2 m.
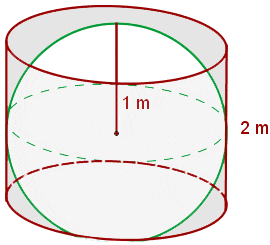
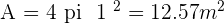
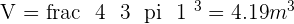
Solution of exercise 16
Calculate the volume of a hemisphere with a radius of 10 cm.

Solution of exercise 17
Calculate the area and volume of the following spherical cap.
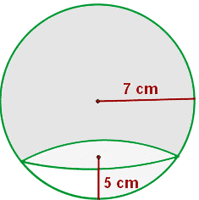
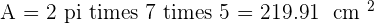

Solution of exercise 18
Calculate the area of the spherical zone and the volume of a spherical segment whose radius circles are 10 and 8 cm and the distance between them is 6 cm.
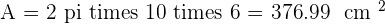

Summarise with AI:













What is frac and sqrt
Interested learning more