Chapters
If you are here, that means you are familiar with polygon, let's take it to a next level. We usually encounter problems related to two-dimensional polygons but what about three-dimensional polygons? In this article, we will talk about three-dimensional polygons.

Polyhedron
One thing is clear that there is not a single polygon. Polygon comes in various shapes and since we are working with polygon, we can conclude that the three-dimensional polygon also comes in various shapes but what do we call a three-dimensional polygon? We will call it a Polyhedron. In many textbooks, you will find this definition, a polyhedron is a three-dimensional region of space bounded by polygons.
Consider the diagram below:
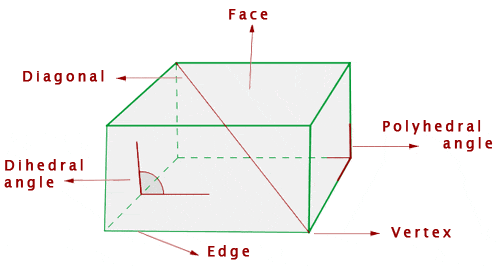
Yes, that is a rectangle but in a three-dimensional region. There is no need to get overwhelmed by the diagram because we are going to make it simple for you. Imagine that you cut a rectangle out of a piece of paper. The rectangle will have a certain length and width. When we talk about three-dimension, we include another parameter and that is called height. In two dimensions, the height of the object is equal to the unit. That is why we don't include this factor because anything multiplied or divided by a unit will remain the same but since we are talking about three-dimension, there will be some height, it can be greater or than unit or maybe less or maybe the same! There is no telling but we will do consider the height when working in the three-dimension.
Let's get back to our track where we were constructing a rectangle in a three-dimensional figure. Keeping the height and width of the rectangle the same, cut more than ten pieces. Stack those pieces together. What do you see? Something like the above picture? Yes, of course, because they both are the same! You can do this for any other polygon since the rectangle isn't the only polygon. There are some terminologies related to a polyhedron, let's take a look at them.
Faces
The faces of a polyhedron are each of the two-dimensional polygons that border the polyhedron.
Edges
The edges of a polyhedron are the sides of the faces of the polyhedron. Two faces have an edge in common.
Vertices
The vertices of a polyhedron are the vertices of each of the faces of the polyhedron. Three faces coincide with the same vertex.
Dihedral Angles
The dihedral angles are formed between two faces of all neighbouring polygons.
Polyhedral Angles
Polyhedral angles are formed by three or more faces of the polyhedron and have a common vertex.
Diagonals
The diagonals of a polyhedron are the line segments joining two vertices not belonging to the same face.
Euler's formula
Euler's formula is used in two places. The first place where this formula is used is in trigonometry and guess the second place? You got it right, Euler's formula is used for polyhedral too. When there are more than one polyhedral then it is called Polyhedra. Euler's formula states that, in convex polyhedra, if you add the number of faces and number of vertices, it will be equal to the number of edges with an addition of 2.
No. of faces + No. of vertices = No. of the edges + 2.
Types of Polyhedron
The concept of the polyhedron is clear, let's move to its types. As mentioned before, polyhedron comes in different shapes and we will talk about them later, currently, we want to talk about generic types of polyhedron. You can categorize polyhedrons into three types.
Convex Polyhedron

Concave Polyhedron
Regular Polyhedra
A regular polyhedron is composed of angles and faces (regular polygons) that are all equal.
Platonic Solids
Platonic solids are no other than convex, regular polyhedrons. This means that these solids are identical in size and shape and not to mention that all the angles, as well as the sides, will be equal. These are the criteria for platonic solids and there are five shapes that fulfil these criteria.
Tetrahedron
Polyhedron of 4 faces.
Pentahedron
Polyhedron of 5 faces.
Hexahedron
Polyhedron of 6 faces.
Heptahedron
Polyhedron of 7 faces.
Octahedron
Polyhedron of 8 faces.
Nonahedron
Polyhedron of 9 faces.
Decahedron
Polyhedron of 10 faces.
Undecahedron
Polyhedron of 11 faces.
Dodecahedron
Polyhedron of 12 faces.
Icosahedron
Polyhedron of 20 faces.
Irregular Polyhedra
An irregular polyhedron is defined by polygons that are composed of elements that are not all equal.













What is frac and sqrt
Interested learning more