Chapters
We all know about squares, all sides equal, vertices having right-angle, etc. The square that we all learned in our early days in geometry was in two-dimension, let's take a step further and talk about three-dimensional figures. The square turns into a cube when we take it into the three-dimensional world. That is why we dedicated this resource to the cube.

What is a Cube
One of the biggest use of this geometrical shape is in making packaging cardboard boxes. If the cardboard box's dimensions are equal in length that means it is a cube. Therefore, the definition of a cube is that it is a regular polyhedron composed of 6 equal squares. Another name of a cube is a regular hexahedron. Check out the below diagram.

That is a perfect cube. As you can see, all the sides are the same and that is an important factor. If any one of the sides is not the same as the other, that shape won't be considered a cube. It can be another polyhedron but not a cube.
Unfold of a Cube
To understand three-dimensional figures more, we need to unfold their secrets. The best way to learn about them is through unfolding them. Let's unfold the figure.
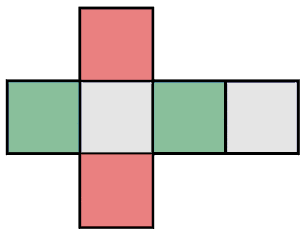
The unfolded cube looks like hopscotch that we all used to play in our childhood, right? We will use this unfolded figure to find the characteristics as well as the surface area of the cube.
Characteristics of a Cube
As mentioned above, the unfolded cube is used to find the characteristics of a cube. Let's figure it out.
The first part you see is the faces of the cubes. Take your time and count how many faces does a cube have. Yes, a cube has six faces.
Number of faces: 6.
Vertices can be found using the cube figure. Vertix is the joining of two points together to form a complex figure.
Number of vertices: 8.
Edges can also be calculated using the cube figure. Take a look at the cube and find the number of edges in a cube.
Number of edges: 12.
Number of concurrent edges at a vertex: 3.
Surface Area of a Cube
Of course, this isn't geometry if you won't be asked to find the surface area or volume of the cube. The surface area of the cube covers all the faces of the unfolded cube.
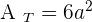
Below is the lateral area of the cube:

Volume of a Cube
The volume of the cube will be the cube(the power cube) of the side of the cube.

Diagonal of a Cube

The diagonal of the cube is the distance between two opposite vertices. To find the diagonal of the cube you need to multiply the side of a cube with the square root of three.
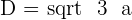
Example
Calculate the diagonal, the lateral area, surface area and volume of a cube with an edge of 5 cm.


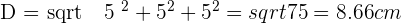


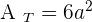
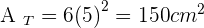

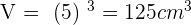













What is frac and sqrt
Interested learning more