Chapters

What are Permutations?
Combinatorial mathematics, also known as combinatorics, is a field of mathematics that involves the problems related to selection, arrangement, and operation inside the discrete or finite system. Permutation and combination are the concepts within the combinatorial mathematics.
Permutations and combinations have many similarities as both the concepts tell us the number of possible arrangements. However, the fundamental difference between the two concepts lies in the order of the elements. In combinations, the order of elements does not matter, whereas in permutations order is important.
Consider a fruit salad that contains apple, bananas, and peaches. Here, we will use the concept of combination to determine the possible outcomes in terms of arrangements. Whereas, when we are given a code such as 45678, the order becomes very important. We cannot shift the position of the digits in this code because code will only work when it is used in the exact order. Here, we will use permutation instead of combination to determine the possible outcomes. Hence, we can also say that the permutation is an ordered combination. When we find combinations and permutations, we usually assume that the items from the set are used or picked without replacement.
Types of permutations
There are two types of permutations:
- Permutations when repetitions are allowed
- Permutation when repetitions are not allowed
When repetition is allowed
It is quite easy to calculate the permutations when repetition is allowed. For instance, consider the following scenario:
In how many ways, three numbers can be selected from the first 10 natural numbers when repetition is allowed?
Since it is mentioned that the repetition is allowed, therefore we will use the following formula to calculate the number of permutations:
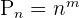
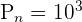

Hence, there are 1000 possible permutations.
When repetition is not allowed
The general formula for the computation of the number of arrangements of objects in a set, i.e. permutations when repetition is not allowed is given below:
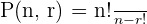
We read n! as n factorial and it describes all elements from 1 to n multiplied together. If the problem entails telling the number of arrangements of all the elements in the set, then we use n! formula.
Consider the following scenario:
Suppose there is a set of 6 beads. In how many ways, 4 beads can be selected from this set without repetition?
In the above scenario, it is given that the 4 beads out of 6 beads will be selected without repetition. Hence, we will substitute the values in the following formula to get the number of possible outcomes:
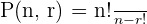
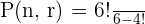


Hence, the beads can be arranged in 360 ways.
Have you ever wondered what is the factorial of the number 0? Well, you will be surprised to know that 0! or zero factorial is equal to 1. In mathematics, zero factorial equates to 1 for the simplification of problems.
Linear vs Circular Permutations
Permutations can also be distinguished by looking at the ways in which elements of a set are arranged. If we find the number of ways in which the elements of the set are arranged in a line, then we say that we are finding a linear permutation.
For example, consider the following scenario:
7 colored balls are arranged in a line. How many different arrangements are possible?
Since we have to arrange all the objects in a set, therefore we will use the following formula of linear permutation:


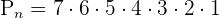
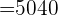
Hence, 7 balls can be arranged in 5040 ways in a line.
Circular permutations
The number of arrangements of the elements around a fixed circle is known as circular or cyclic permutation. There are two types of circular permutation:
- When clockwise and anticlockwise orders are different
- When clockwise and anticlockwise orders are the same
When clockwise and anti-clockwise orders are different
When clockwise and anticlockwise orders are different, then we use the following formula to calculate the permutations:
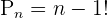
Consider the following example:
Suppose 7 students are sitting around a circle. Calculate the number of permutations if clockwise and anticlockwise arrangements are different.
In the above scenario, you should use the following circular permutation formula. This formula is for finding all possible combinations of elements in a circle when clockwise and anticlockwise arrangements are different.
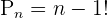
Substitute the values in the above formula to get the number of combinations:
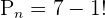
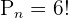

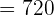
Hence, there are 720 possible arrangements of 7 students around a circle, given the fact that clockwise and anticlockwise arrangements are different.
When clockwise and anticlockwise orders are the same
If clockwise and anticlockwise arrangements are the same, then we use the following formula to calculate the permutations:
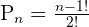
Here:
 means circular permutation
means circular permutation
n represents the number of objects in a set
In this case, the number of possible permutations in a circle are simply divided by 2 factorial.
Consider the following scenario:
Suppose 7 students are sitting around a circle. Calculate the number of permutations if clockwise and anticlockwise arrangements are the same.
In the above scenario, you should use the following circular permutation formula. This formula is for finding all possible combinations of elements in a circle when clockwise and anticlockwise arrangements are the same.
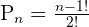
Substitute the values in the above formula to get the number of combinations in a circle:
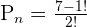
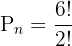
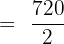

Hence, there are 360 permutations if 7 students are sitting around a circle given that the clockwise and anticlockwise arrangements are the same.
Now, that you know what are the circular permutations and their formulas in two scenarios, let us proceed to solve some more examples.
Example 1
How many different arrangements of 8 balls are possible in a circle, given that the clockwise and anticlockwise arrangements are different?
Solution
Since the balls are arranged in a circle with a condition that the clockwise and anticlockwise arrangements are different, therefore we will use the following circular permutations formula to calculate the number of possible arrangements.
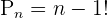
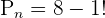

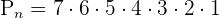
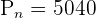
Hence, 5040 different combinations are possible of 8 balls in a circle, given the fact that the clockwise and anticlockwise arrangements are different.
Example 2
How many different arrangements of 10 balls are possible in a circle given that the clockwise and anticlockwise arrangements are different?
Solution
Since the balls are arranged in a circle with a condition that the clockwise and anticlockwise arrangements are different, therefore we will use the following circular permutations formula to calculate the number of possible arrangements.
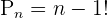


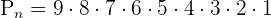
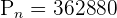
Hence, 362,880 different combinations are possible of 10 balls in a circle, given the fact that the clockwise and anticlockwise arrangements are different.
Example 3
How many different arrangements of 5 students are possible in a circle, given that the clockwise and anticlockwise arrangements are the same?
Solution
Since the balls are arranged in a circle with a condition that the clockwise and anticlockwise arrangements are the same, therefore we will use the following circular permutations formula to calculate the number of possible arrangements.
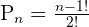
Now, we will substitute the values in the above formula:
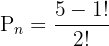
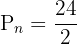
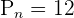
Hence, 12 different arrangements of 5 students are possible in a circle, given the fact that clockwise and anticlockwise arrangements are the same.
Summarise with AI:













Binomial theorem’s and permutation and combination’s
Hi there! Thanks for your comment! The topics of the binomial theorem, permutations, and combinations are all closely related — great concepts to explore together!
Is problem 5 correct?
The last part is 10! Divided by 4!5!.
Thanks for your comment! 😊 You’re right to double-check that step — it’s great to see such careful attention. In this case, the expression 10!/(4!5!) doesn’t apply to this particular problem, as it represents a combination rather than the arrangement described. The correct solution is shown in the explanation above, and we’ve double-checked that problem 5 is correct as written.
Thanks again for taking the time to point it out!
Amazing content
It really help a lot to me…keep it up..
I need some solutions for numbers
Exercises 1 to 12 have covered the different types of combinations.
Bravo for the exercises.
Thanksssss