Chapters

Probability Theory
There is one highly dangerous, legally contentious way to win millions with statistics: by counting cards. You’ve probably heard of the term “counting cards” in various movie plots, which is a card game strategy that uses one of the most important ideas in statistics: probability theory.
Probability is involved in inferential statistics. The difference between descriptive and inferential statistics can be seen through the goals of each branch. While descriptive statistics seeks to understand and visualize what is inside the data set, inferential statistics is used to make predictions using a data set about values outside of it.
Probability theory is a branch of mathematics that deals with random events. Classic examples include the roll of a dice or the toss of a coin - both events which have random distributions. Using a random distribution, you can make predictions about a random event using probability.
In order to get to the point of making predictions, however, you should first start with the basics of probability. This includes some basic definitions:
- Random experiment: an experiment whose outcome cannot be predicted until observed
- Random variable: variable whose values are outcomes of a random experiment
- Sample space: the set of all possible outcomes of a random experiment
- Probability: the likelihood that an event will occur from a random experiment
Combinations and Permutations
Let’s go back to that example from the beginning about counting cards. How exactly is it possible to predict the cards that the player or the dealer will get? One of the ways you can do this is by “counting” the number of possible outcomes.
Sound familiar? This process is simply determining the probability of certain cards being dealt. In fact, a deck of playing cards and its various probabilities is a classic example within probability mathematics.
When you’re interested in understanding the number of outcomes an event can have, the most basic operations you can perform are combinations and permutations. The main difference between the two is that:
- Combination: order does not matter
- Permutation: order does matter
Each can be calculated with and without repetition. Find the formulas and examples of each in the table below.
| Permutation with repetition | A phone has a 4 digit unlock code, with 10 numbers to choose from (0-9) |  |
| Permutation without repetition | In a sporting event, 20 teams can be awarded 1st, 2nd and 3rd place | 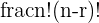 |
| Combination with repetition | A deck of playing cards has 52 cards, of which you are dealt 5 |  |
| Combination without repetition | A popular video app has 1,000 new uploads a day, you see about 30 videos a day. Once you see a video, the app doesn’t show you the same one again | 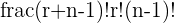 |
The notation simply means that there are n different types of things, of which we can choose those things r times. For permutations with repetitions, this would mean that:
- n is the different types of numbers, 10 of them
- r is the amount we can choose of them, 4 of the 10 numbers
The reason why this is a permutation with repetition, as opposed to without, is because you can have a code with repeating numbers. It is a permutation and not a combination because the order matters - you can only unlock your phone with the correct order of the right numbers. This means that we can calculate all possible phone unlock codes by simply plugging these numbers into the equation.

[
10^4 = 10,000 ;different ; combinations
]

Problem 1
Let’s take the example from the table above. You are obsessed with a popular video app and are curious to know how many different video combinations you get to watch. The site uploads 100 new videos at the beginning of each day and you see about 5.
Once you see a video on the app, the program doesn’t show you the same one again. How many different video combinations are possible?
Problem 2
Let’s take another example from the table above. There are 20 teams competing in the upcoming championship. There are only three prizes awarded at the end of the tournament: 1st, 2nd and 3rd place.
You’re interested in determining how many different possible combinations there are for teams winning these prizes. Calculate the possible set of outcomes using the information in the lesson.
Problem 3
You are tasked with coming up with a six-digit passcode that uses only the numbers 0 through 9. The security of this passcode is the first priority. In order to build a strong password, you want to understand the difference in the possible combinations with and without repetition.
Calculate all possible passcodes if you were to use passcodes with repeating digits and without repeating digits and make a statement about which type of passcode would be better for completing your task.
Solution Problem 1
In this problem, you were asked to:
- Calculate the set of all possible outcomes if you see 30 videos in one day
First, we categorize the information we are given by the information we were given earlier in the lesson.
| Combination | This is a combination because order does not matter. | The app can show us any order of videos |
| Without Repetition | This is a combination without repetition | The app doesn’t show us any one video twice |
| n | n = 100 | There are 100 different, new videos on the app on a given day |
| r | r = 5 | We choose 5 to watch on a given day |
So, in order to calculate the possible set of outcomes, we simply have to plug each number into the formula. Take a look at the table below for a step-by-step solution.
| (r+n-1)! | r! | (n-1)! |
| (5+100-1)! =1.03E+166 | 5! = 120 | (100-1)! = 9.33E+155 |
[
dfrac{1.03E + 166}{2120*9.33E+155} = 91,962,520
]
That gives us about 90 million different combinations, and that’s with only 100 new videos. Imagine what that number would be with 1,000 or even 1 million new uploads every day.
Solution Problem 2
In this problem, you were asked to:
- Calculate the set of all possible winning teams given that there are 20 teams
First, we need to break down the information we are given so that our task of calculation is easier.
| Permutation | This is a permutation because order does matter | There can only be one order in which teams win: 1st, 2nd and 3rd place |
| Without repetition | This is a permutation without repetition | One team can’t win both 1st and 2nd place |
| n | n = 20 | There are 20 total teams |
| r | r = 3 | We choose only 3 teams out of all possible teams |
The calculation of this problem is laid out in the table below.
| n! | (n-r)! |
| 2.43E+18 | (20-3)! = 3.56E+14 |
[
dfrac{2.43E+18}{3.56E+14} = 6840
]
There are 6,840 different possible winning team combinations with these 20 teams.
Solution Problem 3
In this problem, you were asked to:
- Calculate the set of possible outcomes of a six digit passcode with and without repetition
- Choose which one would make a more secure passcode
It can be helpful to first organize the information we’ve received into categories based on what was taught in the lesson.
| Permutation | This is a permutation because order matter | The order which you enter the passcode does matter |
| With and Without Repetition | We will calculate with and without repetition | We want to know which passcode will have more combinations |
| n | n = 10 | There are 10 digits we can choose from, going from 0 to 9 |
| r | r = 6 | There are 6 digits we will choose to create our passcode |
Below, we’ve calculated each type of permutation.
| Permutation with Repetition | 10^6 | 1,000,000 |
| Permutation without Repetition | 10!/(10-6)! | 151,200 |
Summarise with AI:













Binomial theorem’s and permutation and combination’s
Hi there! Thanks for your comment! The topics of the binomial theorem, permutations, and combinations are all closely related — great concepts to explore together!
Is problem 5 correct?
The last part is 10! Divided by 4!5!.
Thanks for your comment! 😊 You’re right to double-check that step — it’s great to see such careful attention. In this case, the expression 10!/(4!5!) doesn’t apply to this particular problem, as it represents a combination rather than the arrangement described. The correct solution is shown in the explanation above, and we’ve double-checked that problem 5 is correct as written.
Thanks again for taking the time to point it out!
Amazing content
It really help a lot to me…keep it up..
I need some solutions for numbers
Exercises 1 to 12 have covered the different types of combinations.
Bravo for the exercises.
Thanksssss