Chapters

Combinatorics Definition
If your name is Oliver or Olivia, chances are you’ve probably met others with your name if you’re living in the UK. According to the Office of National Statistics, Oliver was the most popular boy name from 2012 to 2018 while Olivia held the same title for girls from 2015 to 2018. In fact, in any given group of people, there are bound to be at least two people with the same name.
What is the probability of two people in a given group sharing the same name, hair colour or birthday? How about the number of ways you can rearrange a given word? These questions and phenomena ultimately fall under one subject within mathematics: combinatorics.
Combinatorics is defined as the branch of mathematics that deals with counting, arranging, selecting and classifying things. At its basis, it can be understood as the study of the possible combinations of things. As you can probably guess, combinatorics is one of the oldest branches of maths, which you can trace from ancient India and China, through the Middle Ages and Enlightenment, up to present day.
Combinatorics has dozens of subfields, some of which you can see listed below:
- Enumerative combinatorics
- Analytic combinatorics
- Graph theory
- Finite geometry
- Geometric combinatorics
Most notably, probabilistic combinatorics is to calculate the expected value, or the mean, of a random variable. In order to understand the basics of combinatorics, you should get familiar with some definitions.
A finite sample space is the random of values for a given random variable. Take phones for example. A company has three models of phones - A12, A13, A14 - which can have either 64GB or 128GB of storage. The sample space for the possible phones a given customer will buy is:
| Model | Storage Space |
| A12 | 64GB |
| A12 | 128GB |
| A13 | 64GB |
| A13 | 128GB |
| A14 | 64GB |
| A14 | 128GB |
As you can see, there are 6 different possible outcomes for this random variable. In this example, we simply have to count all the different combinations of phones a customer can buy. However, this is only practical if there aren’t that many combinations. For problems with hundreds or thousands of different outcomes, the multiplication principle is useful.
The multiplication principle deals with a random number of experiments. It states that if there are m ways of doing one thing and n ways to do another, there are many ways to do both. Taking our example above, if:
- m = 3 phone models
- n = 2 storage capacities
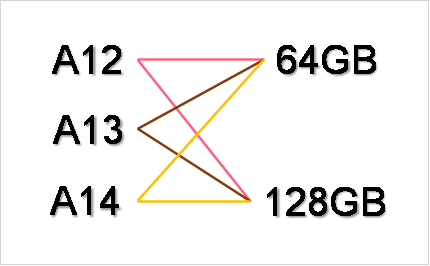
Then there are 3 x 2 = 6 different combinations of both m and n. This can be used regardless of the number of things you are combining. If you were to add colour to the phone example, say gold and black, you can calculate:
- m = 3
- n = 2
- l = 2 phone colours
Then there are now 3 x 2 x 2 = 12 different phone combinations.

Combinatorics and Probability
Combinatorics and probability intersect at two of the most important concepts inside of counting: combinations and permutations. While the basics of the counting principle are easy to grasp, there are a couple of definitions you should learn before going over combinations and permutations.
The first is the notation and definitions for combinations and permutations, which can be found summarized in the table below.
| Description | Notation | |
| Permutation with repetition | You choose r amount of n things, where r can be repeating digits. The order of these digits matters. | 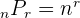 |
| Permutation without repetition | You choose r amount of n things, where r cannot be repeating digits. The order of these digits matters. | 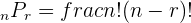 |
| Combination with repetition | You choose r amount of n things, where r can be repeating digits. The order of these digits does not matter. |  |
| Combination without repetition | You choose r amount of n things, where r cannot be repeating digits. The order of these digits does not matter. | 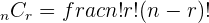 |
If you’re worried about understanding the notation, the step-by-step examples in the next sections will help clear it up. What you may notice, and what will be addressed here, are the exclamation points in each formula.
These are known as factorials. Factorials are relatively easy to understand, which is great because they are vital to calculating combinations and permutations. The exclamation point is a factorial function, which means that you should multiply all whole numbers starting from the number before the factorial all the way down to 1.
For example, 3! Is equal to
[
3*2*1 = 6
]
Notice that we start with 3 and multiply every whole number below 3 down to 1. Take a look at the table below for some more examples.
| 4! | 4*3*2*1 = 24 |
| 5! | 5*4*3*2*1 = 120 |
| 6! | 6*5*4*3*2*1 = 720 |
Step-by-Step Problem Combination
A combination, as we can see from the definitions table above, is a set of outcomes where order does not matter whose formulas are:
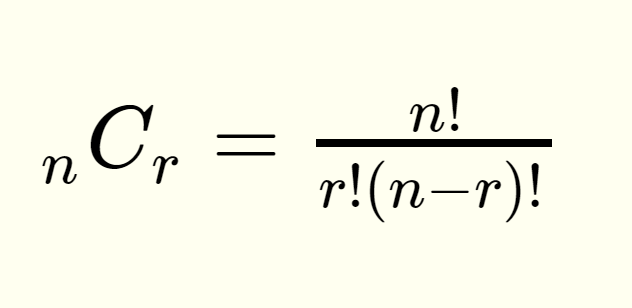
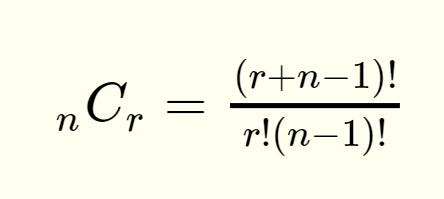
Let’s take a look at one example of a combination and break it down both with and without repetition. One classic example involves ice cream. Say that your local ice cream shop has five different flavours, which you can choose two of. What are the possible combinations of flavours you can get if order doesn’t matter?
Take a look at some of the possible combinations written down below if each flavour is marked A through E.
| With Repetition | Without Repetition |
| A, B A, C A, D A, E B, C B, D B, E C, D C, E D, E A, A B, B C, C D, D E, E | A, B A, C A, D A, E B, C B, D B, E C, D C, E D, E |
Notice that allowing for repeating flavours gives five more combinations than not allowing for repeating flavours. Another interesting thing to note is that, because order doesn’t matter, these two flavour combinations are the same:
- A, B
- B, A
This is because the order in which we pick the flavours doesn’t matter. Even if you picked vanilla first then strawberry second or strawberry then vanilla, either way you have the same thing on your ice-cream cone.
While it was easy to see all the different combinations here, it would be incredibly time consuming if we were working with larger numbers. Say that instead of just five flavours, we have 12 different flavours to choose from. In this case, it would be much easier to plug the numbers into the equation.
The notation simply means that we have n things of which we choose r amount from. This is read as “n choose r”. In this new example, we have 12 flavours of which we can choose 2 from, meaning n = 12 and r = 2. Now, we can calculate the combinations with and without repetition below.
| With Repetition | Without Repetition | |
| 5 Flavours |   15 | 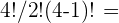 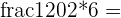 10 |
| 12 Flavours | 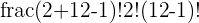 = 78 = 78 |  = 66 = 66 |
Step-by-Step Problem Permutation
Now let’s look at permutations. Recall that the formulas for permutations with and without repetition are:
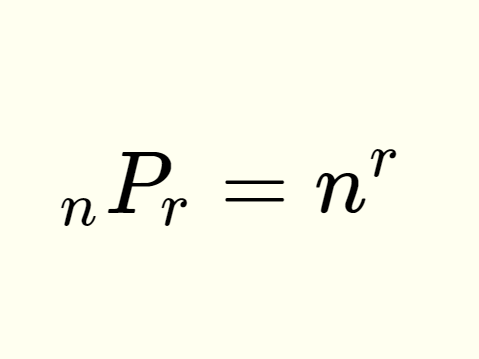
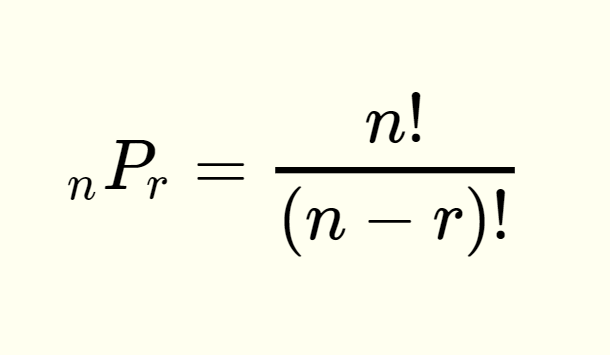
Let’s look at another classic example, which deals with passcodes. Say that you have a two digit passcode that uses a combination of letters from A to D. Take a look at all the possible passcodes we can create with and without repetition.
| With Repetition | Without Repetition |
| A, B A, C A, D B, A B, C B, D C, A C, B C, D D, A D, B D, C A, A B, B C, C D, D | A, B A, C A, D B, A B, C B, D C, A C, B C, D D, A D, B D, C |
Notice that now, because order matters, the following two combinations are not the same:
- A, B
- B, A
This is because with passcodes, order is vital. If your passcode is A, B, the order B,A won’t unlock whatever you are trying to unlock.
Again, instead of writing down all these combinations, we can simply plug them into the equations for permutations with and without repetition.
| With Repetition | Without Repetition | |
| 4 letters |  = 16 = 16 |  = =
|
| 12 letters |  = 144 = 144 | 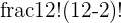 = 132 = 132 |
Summarise with AI:










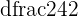 = 12
= 12


Binomial theorem’s and permutation and combination’s
Hi there! Thanks for your comment! The topics of the binomial theorem, permutations, and combinations are all closely related — great concepts to explore together!
Is problem 5 correct?
The last part is 10! Divided by 4!5!.
Thanks for your comment! 😊 You’re right to double-check that step — it’s great to see such careful attention. In this case, the expression 10!/(4!5!) doesn’t apply to this particular problem, as it represents a combination rather than the arrangement described. The correct solution is shown in the explanation above, and we’ve double-checked that problem 5 is correct as written.
Thanks again for taking the time to point it out!
Amazing content
It really help a lot to me…keep it up..
I need some solutions for numbers
Exercises 1 to 12 have covered the different types of combinations.
Bravo for the exercises.
Thanksssss