When we hear the word "combination" in our daily life, we immediately think about the collection of things in the form of a set or a group. For instance, if anyone says that my bowl has a combination of apples, carrots, and bananas, then we immediately think that the bowl has three items. We are not concerned with the order in which these three things were put in the bowl.
In mathematics, combination means the number of ways in which different objects are combined to form a set. For combinations, the order of elements is not important.
We always study combinations with permutations in mathematics because there are many similarities between these two terms. The primary difference between the combination and permutation is that the order matters in permutation, while it does not matter in combination. In other words, we can say that the permutation is an ordered combination.
| Permutation 🔢 | Combination 🔢 | |
|---|---|---|
| Order matters | ✅ Yes, order matters | ❌ No, order doesn’t matter |
| Repetition | Can be with or without repetition | Usually without repetition |
| Formula | Without repetition: P(n,r) = n!/(n-r)! With repetition: n^r | C(n,r) = n!/(r!(n-r)!) |
| Example | Arranging 3 letters A, B, C in 2 positions: AB ≠ BA | Choosing 2 letters from A, B, C: AB = BA |
You have already read an example of a simple combination above when three things are put in a bowl. Now, let us consider another scenario.
Harry wants to make a PIN code by choosing 4 digits from the set of the first five whole numbers (0,1,2,3,4). Suppose his chosen PIN code is 4013. Can he rearrange the digits as 3014 or 0143, etc.?
Of course not, the order of the digits is important. If the order of the digits is changed, then the PIN code will not work. It means that the selection of code from the first five whole numbers is an example of a permutation.

Types of Permutations
There are two types of permutations:
Elements can be repeated in each arrangement.
Used when the same item can appear more than once.
Each element can be used only once.
Used when items cannot be repeated.
In this article, we will specifically discuss permutations with repetition.
Permutations with Repetition
We know that in the permutations, the order of elements is important. Permutations with repetition mean we can select one item twice. The formula for computing the permutations with repetitions is given below:

Here:
n = total number of elements in a set
k = number of elements selected from the set
Consider the following example:
From the set of the first 10 natural numbers, you are asked to make a four-digit number. How many different permutations are possible?
First, we need to determine whether we can choose a digit twice or not. We can have four-digit numbers such as 1000, 1002, 3032, and 4044. In all these numbers, one digit is repeated twice or thrice. Therefore, it means that it is an example of permutations with repetition.
The total number of elements in a set is 10, and the number of digits we want to select from this set is 4. Therefore, we will get permutations by substituting the values in the following formula:

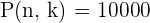
Hence, 10000 permutations are possible if we want to make a four-digit number from the set of the first 10 natural numbers.
Sometimes we are given a problem in which the identical items of type 1 are repeated "p" number of times, type 2 are repeated "q" number of times, type 3 are repeated "r" number of times, and so on. The question arises, what shall we do in this case? Well, the answer is simple. There is a separate formula to compute permutations in such problems.
Since the items are repeated, such scenarios are also examples of permutations with repetition. The formula that should be used while computing the permutations in such cases is given below:
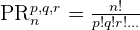
Let us solve the following example through the above formula to make the whole concept clearer.
How many eight-digit numbers can be formed with the numbers 2, 2, 2, 3, 3, 3, 4, 4?
Here, n = 8, p = 3, q = 3, and r = 2.
In this example, the order of elements matters, and digits are repeated. We will substitute the above values in the formula below:

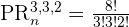
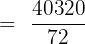
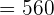
Hence, 560 permutations are possible.
Permutation Example Problems
In how many ways can the letters of the word EXCELLENT be arranged?
Total number of elements in the word = n = 9
E is repeated three times, hence p = 3
L is repeated 2 times, hence q = 2
Substitute these values in the formula below to get the number of ways in which the letters of this word can be arranged:



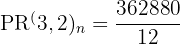

Hence, the letters in the word EXCELLENT can be arranged in 30240 ways.
A ship must raise eight flags at one time (two red, two blue, and four green). How many different flag combinations can be raised at a time?
Here:
The total number of flags = n = 8
Number of red flags = p = 2
Number of blue flags = q = 2
Number of green flags = r = 4
This is an example of permutation with repetition because the elements of the set are repeated and their order is important.
Put the above values in the formula below to get the number of permutations:

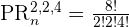
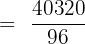

Hence, flags can be raised in 420 ways.
John owns a six-colored pair of shoes (two red, two blue and two black). He wants to put all these pairs of shoes on the shoe rack. How many different arrangements of shoes are possible?
The total number of pair of shoes = n = 6
Number of red shoes = p = 2
Number of blue shoes = q = 2
Number of back shoes = r = 2
This is an example of permutation with repetition because the elements are repeated and their order is important.
Put the above values in the formula below to get the number of permutations:


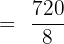

Hence, shoes can be arranged on the shoe rack in 90 ways.
In how many ways can the letters of the word ELECTRIC can be arranged?
Total number of elements in the word = n = 8
E is repeated three times, hence p = 2
C is repeated 2 times, hence q = 2
Substitute these values in the formula below to get the number of ways in which the letters of this word can be arranged:




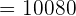
Hence, the letters in the word ELECTRIC can be arranged in 10080 ways.
A person has to choose three digits from the set of the following seven numbers to make a three-digit number.
{1, 2, 3, 4, 5, 6, 7}
How many different arrangements of the digits are possible?
A three-digit number can have 2 or three identical numbers. Similarly, in a number, the order of digits is important.
It is given that the person can select 3 digits from the set of 7 numbers. Hence, n = 7 and k = 3. Substitute these values in the formula below to get the number of possible arrangements.
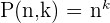
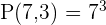

Hence, 343 different arrangements are possible.
Summarise with AI:













Binomial theorem’s and permutation and combination’s
Hi there! Thanks for your comment! The topics of the binomial theorem, permutations, and combinations are all closely related — great concepts to explore together!
Is problem 5 correct?
The last part is 10! Divided by 4!5!.
Thanks for your comment! 😊 You’re right to double-check that step — it’s great to see such careful attention. In this case, the expression 10!/(4!5!) doesn’t apply to this particular problem, as it represents a combination rather than the arrangement described. The correct solution is shown in the explanation above, and we’ve double-checked that problem 5 is correct as written.
Thanks again for taking the time to point it out!
Amazing content
It really help a lot to me…keep it up..
I need some solutions for numbers
Exercises 1 to 12 have covered the different types of combinations.
Bravo for the exercises.
Thanksssss