Chapters
In this article, you will learn what is Pascal's triangle and its properties. You will also learn how to use its formula to find its values or entries in specific rows and columns and use its values to expand complex binomial expressions.

What is a Pascal Triangle?
Pascal's Triangle is a number pattern that is named after a notable French mathematician and philosopher, Blaise Pascal. To build a pascal's triangle, we start with 1 at the top of the triangle, and then we put numbers below 1 in a triangular pattern. Consider the figure below that shows Pascal's triangle.
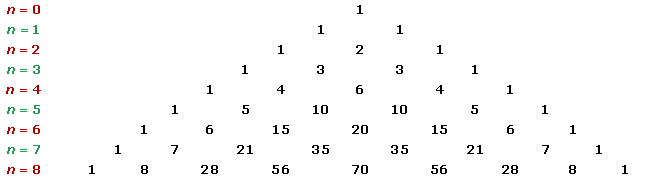
To build the triangle, start with "1" at the top, then continue placing numbers below it in a triangular pattern. Each number below is obtained by adding the numbers above it. Pascal's triangle is a triangle of integers that is not only symmetrical but also infinite. It is symmetrical because the left side of the triangle is a mirror image of the right side. It means that the numbers on the left side are the same as the numbers on the right side.
For example, you can see in Figure 1.1 that the numbers on the left and right sides of the triangle are identical. You will also notice the fact that the numbers below are obtained by adding the two numbers directly above it.

In the above figure, the numbers below are obtained by adding the two diagonal numbers above it. For example, 21 = 16 + 5 and 15 = 10 + 5.
Pascal's Triangle Formula
There is a formula to determine the value in any row of Pascal's triangle. But before proceeding to the formula, you should know that the first row and the first column have zero values. The topmost row of Pascal's triangle is row "0" and the leftmost column in the triangle is column "0". This phenomenon is shown in the following triangle.
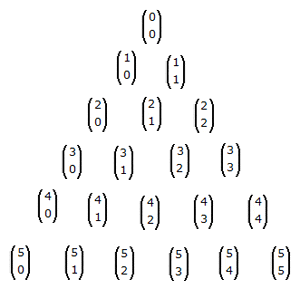
You can see that the topmost row is zero and since it is the first column of the row, therefore the column is also zero. It is mathematically denoted as  . It can be read as 0 choose 0.
. It can be read as 0 choose 0.
Any entry in Pascal's triangle can be determined by using the following formula:

Here:
 is read as n choose k. It is the binomial coefficient.
is read as n choose k. It is the binomial coefficient.- ! symbol represents factorial.
- n represents the row and k represents the column
Pascal's Triangle Properties
Some of the properties of Pascal's triangle are given below:
- Pascal's triangle is an infinite sequence of numbers in which the top number is always 1. The second line reflects the combinatorial numbers of 1, the third one of 2, the fourth one of 3, and so on.
- The starting and ending entry in each row is always 1.
- All rows in this triangle are symmetrical.
- Each number is obtained by adding the two numbers above it (diagonally). This pattern resembles the Fibonacci sequence in which each subsequent number is the result of the addition of two previous numbers.
- Pascal's triangle is useful in computing the coefficients of the Binomial theorem. For example, the
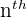 row of Pascal's triangle has the coefficients of the expanded polynomial
row of Pascal's triangle has the coefficients of the expanded polynomial  .
. - In the second diagonal of Pascal's triangle, the square of the number is equal to the sum of the next number and the number below it. For example, see figure 1 and take the number 5 from the second diagonal. Its square is equal to the addition of the number next to it which is 10 and the number 15 that is below it. Mathematically, we can write it as
 .
. - If you highlight the odd and even numbers in Pascal's triangle, you will get a new pattern that will resemble Sierpinski Triangle.
In the next section, we will use Pascal's triangle formula to determine the values in the triangle.
Example 1
What are the values of:
a. 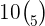
b. 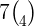
c. 
d. 
e. 
Solution
a. 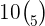
10 in the above expression reflects the row number and 5 represents the column number. It means that we have to tell the value in  row and
row and 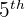 column.
column.
Use the following formula to determine this value:

Substitute n = 10 and k = 5 in the above formula:
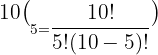

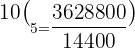
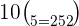
Hence, in a pascal's triangle the value in the 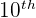 row and
row and 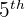 column is 252.
column is 252.
b. 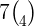
7 in the above expression reflects the row number and 4 represents the column number. It means that we have to tell the value in  row and
row and 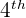 column.
column.
Use the following formula to determine this value:

Substitute n = 7 and k = 4 in the above formula:
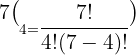
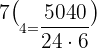
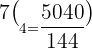
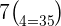
Hence, in a pascal's triangle the value in the 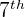 row and
row and 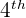 column is 35.
column is 35.

 row and
row and 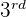 column. Use the following formula to determine this value:
column. Use the following formula to determine this value: 
Substitute n = 4 and k = 3 in the above formula:
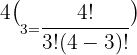

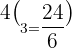

Hence, in a pascal's triangle the value in the 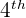 row and
row and 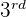 column is 4.
column is 4.

 row and
row and 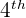 column. Use the following formula to determine this value:
column. Use the following formula to determine this value: 
Substitute n = 5 and k = 4 in the above formula:
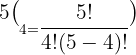
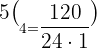


Hence, in a pascal's triangle the value in the 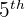 row and
row and 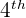 column is 5.
column is 5.

 row and
row and 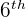 column. Use the following formula to determine this value:
column. Use the following formula to determine this value: 
Substitute n = 9 and k = 6 in the above formula:
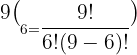
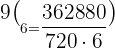
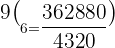
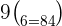
Hence, in a pascal's triangle the value in the  row and
row and 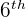 column is 84.
column is 84.
Example 2
Using Pascal's triangle expand the polynomial 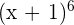 .
.
Solution
We know that the coefficients of this expanded polynomial will be the 6th row of Pascal's triangle. For example, consider the figure 1.1. The sixth row has the coefficients 1, 6 , 15, 20, 15, 6 and 1. Using these coefficients, we can expand the polynomial like this:
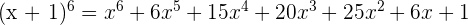
Example 3
Using Pascal's triangle expand the polynomial  .
.
Solution
We know that the coefficients of this expanded polynomial will be the 7th row of Pascal's triangle. For example, consider the figure 1.1. The seventh row has the coefficients 1, 7 , 21, 35, 35, 31, 7 and 1. Using these coefficients, we can expand the polynomial as:

Summarise with AI:













Binomial theorem’s and permutation and combination’s
Hi there! Thanks for your comment! The topics of the binomial theorem, permutations, and combinations are all closely related — great concepts to explore together!
Is problem 5 correct?
The last part is 10! Divided by 4!5!.
Thanks for your comment! 😊 You’re right to double-check that step — it’s great to see such careful attention. In this case, the expression 10!/(4!5!) doesn’t apply to this particular problem, as it represents a combination rather than the arrangement described. The correct solution is shown in the explanation above, and we’ve double-checked that problem 5 is correct as written.
Thanks again for taking the time to point it out!
Amazing content
It really help a lot to me…keep it up..
I need some solutions for numbers
Exercises 1 to 12 have covered the different types of combinations.
Bravo for the exercises.
Thanksssss