Chapters
In mathematics, permutations represent the number of ways to arrange a set of distinct objects in a specific order.
The order matters — that’s what differentiates permutations from combinations.
For example, arranging the letters A, B, and C gives six possible orders:
ABC, ACB, BAC, BCA, CAB, and CBA.
The general formula for permutations is: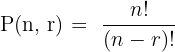
where
n = total number of objects
r = number of objects selected
! = factorial (the product of all positive integers up to that number)

Practice Problems and Solutions
How many different 4-letter words can be formed using the letters of the word MATH, if all letters are used?
There are 4 distinct letters.
The number of possible arrangements is:

Answer: 24 possible arrangements
How many 5-digit numbers can be formed using the digits 1, 2, 3, 4, 5, 6, 7, 8, without repetition?
We are selecting 5 digits from 8, order matters, no repetition.
So:
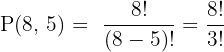
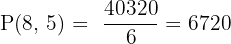
Answer: 6720 possible 5-digit numbers
How many different words can be formed using all the letters of the word BANANA?
The total number of letters = 6
There are repeating letters:
A appears 3 times, N appears 2 times.
Hence:
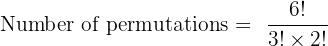

Answer: 60 distinct arrangements of BANANA
Eight people are to stand in a row for a photograph. If two friends must always stand together, how many possible arrangements are there?
Treat the two friends as one single unit.
Then, we have 8−1=7 total units to arrange.
These 7 can be arranged in:
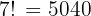
The two friends can switch places with each other in:
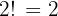
Total arrangements:
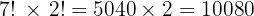
Answer: 10080 possible arrangements
In how many ways can the letters of the word COMPUTER be arranged if the vowels must always be together?
Letters in COMPUTER = 8 total
Vowels: O, U, E → 3 vowels (to be grouped together)
Treat the 3 vowels as one unit, so we have:

These 6 units can be arranged in:
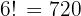
The 3 vowels can be arranged among themselves in:
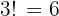
Total arrangements:
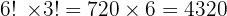
Answer: 4320 arrangements with vowels together
A lock has 5 keys, all distinct. In how many ways can the keys be arranged on a key ring?
When arranging around a ring (circular permutation):
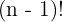
Substitute n=5:
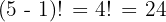
Answer: 24 possible circular arrangements
How many different 7-digit numbers can be formed from the digits 1, 2, 3, 4, 5, 6, 7
if the number must start with an odd digit?
Odd digits: 1, 3, 5, 7 → 4 possible starting digits
After choosing the first digit, the remaining 6 digits can be arranged in:
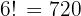
Total possibilities:
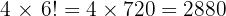
Answer: 2880 possible 7-digit numbers
From a group of 8 students, how many ways can we select a president, vice-president, and secretary, if no person can hold more than one position?
Order matters (because the roles are distinct).
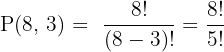
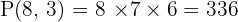
Answer: 336 possible ways to assign the positions
How many distinct arrangements of the word MISSISSIPPI are there?
There are 11 total letters.
M → 1
I → 4
S → 4
P → 2
So:
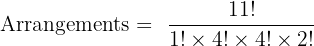

Answer: 34650 distinct arrangements of MISSISSIPPI
How many different ways can 4 people be arranged in a line such that Alice is always ahead of Bob?
Total arrangements of 4 people:
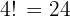
Half of these will have Alice ahead of Bob, and the other half will have Bob ahead of Alice.
So:
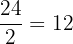
Answer: 12 possible arrangements where Alice is ahead of Bob
Summarise with AI:












Binomial theorem’s and permutation and combination’s
Hi there! Thanks for your comment! The topics of the binomial theorem, permutations, and combinations are all closely related — great concepts to explore together!
Is problem 5 correct?
The last part is 10! Divided by 4!5!.
Thanks for your comment! 😊 You’re right to double-check that step — it’s great to see such careful attention. In this case, the expression 10!/(4!5!) doesn’t apply to this particular problem, as it represents a combination rather than the arrangement described. The correct solution is shown in the explanation above, and we’ve double-checked that problem 5 is correct as written.
Thanks again for taking the time to point it out!
Amazing content
It really help a lot to me…keep it up..
I need some solutions for numbers
Exercises 1 to 12 have covered the different types of combinations.
Bravo for the exercises.
Thanksssss