Combination word problems are a fundamental aspect of combinatorics, often featured in GCSE and A-Level mathematics exams. These problems require you to determine how many ways you can select a subset from a larger set, where the order of selection does not matter. Mastering these problems is crucial for achieving top marks in your exams.

What Is a Combination?
In mathematics, a combination is a selection of items from a larger set, where the order of selection is irrelevant. The number of ways to choose r items from a set of n distinct items is given by the combination formula:
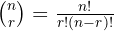
Where:
- n is the total number of items
- r is the number of items to choose
- ! denotes a factorial
This formula calculates the number of possible combinations without repetition.
Solving Combination Word Problems
How many different combinations of management can there be to fill the positions of president, vice-president and treasurer of a football club, knowing that there are 12 eligible candidates?
How many different combinations of management can there be to fill the positions of president, vice-president and treasurer of a football club knowing that there are 12 eligible candidates?
The order of the elements does matter.
The elements cannot be repeated.
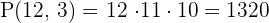
How many different ways can the letters in the word "micro" be arranged if it always has to start with a vowel?
How many different ways can the letters in the word "micro" be arranged if it always has to start with a vowel?
The words will begin with i or o followed by the remaining 4 letters taken from 4 by 4.
The order of the elements does matter.
The elements cannot be repeated.

How many combinations can the seven colours of the rainbow be arranged into groups of three colours each?
How many combinations can the seven colours of the rainbow be arranged into groups of three colours each?
The order of the elements does not matter.
The elements cannot be repeated.
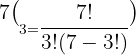
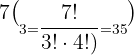
How many different five-digit numbers can be formed with only odd numbered digits? How many of these numbers are greater than 70,000?
How many different five-digit numbers can be formed with only odd numbered digits? How many of these numbers are greater than 70,000?
The order of the elements does matter.
The elements cannot be repeated.
n = 5 k = 5

How many games will take place in a league consisting of four teams? (Each team plays each other twice, once at each teams respective "home" location)
How many games will take place in a league consisting of four teams? (Each team plays each other twice, once at each teams respective "home" location)
The order of the elements does matter.
The elements cannot be repeated.
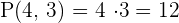
10 people exchange greetings at a business meeting. How many greetings are exchanged if everyone greets each other once?
10 people exchange greetings at a business meeting. How many greetings are exchanged if everyone greets each other once?
The order of the elements does not matter.
The elements cannot be repeated.

How many five-digit numbers can be formed with the digits 1, 2 and 3? How many of those numbers are even?
How many five-digit numbers can be formed with the digits 1, 2 and 3? How many of those numbers are even?
The order of the elements does matter.
The elements are repeated.
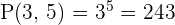
If the number is even it can only end in 2.
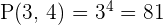
How many lottery tickets must be purchased to complete all possible combinations of six numbers, each with a possibility of being from 1 to 49?
How many lottery tickets must be purchased to complete all possible combinations of six numbers, each with a possibility of being from 1 to 49?
The order of the elements does not matter.
The elements cannot be repeated.
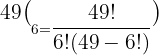
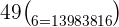
How many ways can 11 players be positioned on a soccer team, considering that the goalie cannot hold another position other than in goal?
How many ways can 11 players be positioned on a soccer team considering that the goalie cannot hold another position other than in goal?
Therefore, there are 10 players who can occupy 10 different positions.
The order of the elements does matter.
The elements cannot be repeated.

How many groups can be made from the word "house" if each group consists of 3 letters?
The word house has 5 alphabets. If each new word should have 3 alphabets, then we should use the following formula:
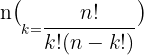 , where
, where 
Substitute the values in this example in the above formula:
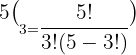
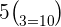
Sarah has 8 colored pencils that are all unique. She wants to pick three colored pencils from her collection and give them to her younger sister. How many different combinations of colored pencils can Sarah make from 8 pencils?
Number of pencils Sarah have = 8
Number of pencils she wants to give to her younger sister = 3
We will use the binomial coefficients formula to determine the number of combinations:
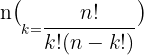 , where
, where 
After substitution we will get the number of combinations:
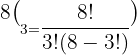
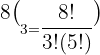
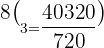

Hence, Sarah can make 56 combinations of 8 coloured pencils, given the fact that she can choose 3 at a time.
Alice has 6 chocolates. All of the chocolates are of different flavors. She wants to give two of her chocolates to her friend. How many different combinations of chocolates can Alice make from six chocolates?
Number of chocolates Alice has = 6
Number of chocolates she wants to give to her friend = 2
We will use the binomial coefficient formula to determine the number of combinations:
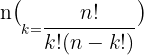 , where
, where 
After substitution, we will get the number of combinations:
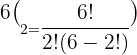
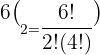
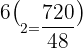
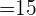
Hence, Alice can make 15 combinations of 6 chocolates, given the fact that she can choose 2.
Summarise with AI:












Binomial theorem’s and permutation and combination’s
Hi there! Thanks for your comment! The topics of the binomial theorem, permutations, and combinations are all closely related — great concepts to explore together!
Is problem 5 correct?
The last part is 10! Divided by 4!5!.
Thanks for your comment! 😊 You’re right to double-check that step — it’s great to see such careful attention. In this case, the expression 10!/(4!5!) doesn’t apply to this particular problem, as it represents a combination rather than the arrangement described. The correct solution is shown in the explanation above, and we’ve double-checked that problem 5 is correct as written.
Thanks again for taking the time to point it out!
Amazing content
It really help a lot to me…keep it up..
I need some solutions for numbers
Exercises 1 to 12 have covered the different types of combinations.
Bravo for the exercises.
Thanksssss