Chapters

Introduction
Have you ever wondered how many possible ways you could arrange your bookshelf, or how many different lottery combinations could be drawn? Combinatorics is the branch of mathematics dedicated to answering these exact questions. It is the art and science of counting without necessarily listing every single possibility.
Whether it is in cryptography (keeping your passwords safe), probability, or computer science, combinatorics allows us to handle complex counting tasks efficiently. By using formulas for factorials, permutations, and combinations, we can calculate millions of possibilities in seconds.
In this article, we will break down the fundamental formulas of combinatorics and practice applying them to real-world scenarios.
1. Factorials
Factorials are the foundation of most counting formulas. A factorial represents the number of ways to arrange a set of n distinct objects in a specific order.
Example:
In a room, there are 5 people and 5 chairs in a row. In how many different orders can the people sit?
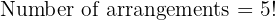
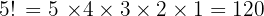
There are 120 different ways to seat the 5 people.
2. Permutations
We use permutations when the order of selection matters. For example, the code "1-2-3" is different from "3-2-1."
a) Permutations with Repetition
Use this when you can pick the same item more than once (like a keycode).
Example: Create a 3-digit code using the digits {0, 1, 2, 3, 4, 5}. If you can repeat digits, how many codes are possible?
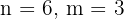
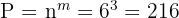
b) Permutations without Repetition
Use this when an item cannot be used twice (like a race where one person cannot finish 1st and 2nd).
Example: In a pool of 10 balls, you choose 5. How many ordered arrangements are possible?
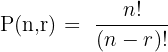
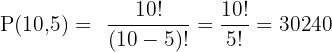
3. Circular Permutations
This refers to arrangements around a fixed circle.
Clockwise and anticlockwise are different: (e.g., people at a table)
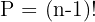
Clockwise and anticlockwise are the same: (e.g., beads on a necklace)
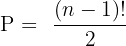
4. Combinations
We use combinations when the order does not matter. Choosing a "group" of friends or a "set" of fruits are combination problems.
a) Combinations without Repetition
Example: A shop has 4 different colored balls. You want to buy 2. How many ways can you choose them?
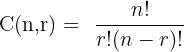
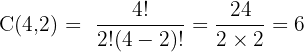
b) Combinations with Repetition
Example: There are 4 ice cream flavours. You are allowed 2 scoops, and you can pick the same flavour twice. How many variations are possible?
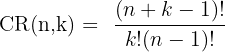
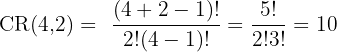
Practice Questions & Solutions
How many different 4-letter "words" (even if they don't make sense) can be formed using the letters in the word "MATH" without repeating any letters?
Since we are arranging all the letters and the order matters, we use the factorial formula.
Step 1: Identify n - there are 4 unique letters: M, A, T, H. So, n = 4.
Step 2: Apply the factorial formula
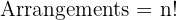
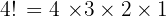
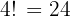
Answer: 24 arrangements.
A club has 12 members. They need to elect a President, a Vice President, and a Treasurer. No person can hold more than one office. How many ways can these positions be filled?
Since the roles are specific (President is different from Treasurer), the order matters. This is a permutation without repetition.
Step 1: n = 12 (total members), r = 3 (positions to fill).
Step 2: Apply the permutation formula
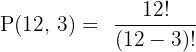
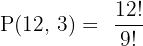
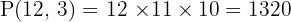
Answer: 1,320 ways.
A pizza shop offers 10 different toppings. If you want to order a pizza with 3 different toppings, how many combinations are possible?
Since the order in which the toppings are put on the pizza does not change the pizza, order does not matter. This is a combination without repetition.
Step 1: n = 10 (toppings), r = 3 (selection).
Step 2: Apply the combination formula
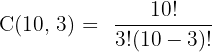
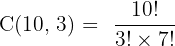
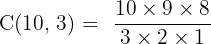
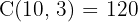
Answer: 120 combinations.
How many ways can 6 people be seated around a circular campfire?
This is a circular permutation problem. Since sitting to someone's left is different from sitting to their right, clockwise and anticlockwise orders are different.
Step 1: n = 6.
Step 2: Apply the circular permutation formula
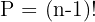
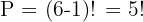
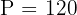
Answer: 120 ways.
A bakery sells 5 types of donuts. You want to buy a box of 3 donuts. If you are allowed to choose multiple donuts of the same type, how many different boxes can you create?
Order does not matter (it’s just a box of donuts), but repetition is allowed. This is a combination with repetition.
Step 1: n = 5 (types), k = 3 (selection).
Step 2: Apply the formula
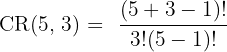
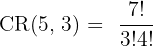
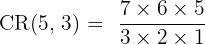
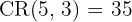
Answer: 35 boxes.
Summarise with AI:












Binomial theorem’s and permutation and combination’s
Hi there! Thanks for your comment! The topics of the binomial theorem, permutations, and combinations are all closely related — great concepts to explore together!
Is problem 5 correct?
The last part is 10! Divided by 4!5!.
Thanks for your comment! 😊 You’re right to double-check that step — it’s great to see such careful attention. In this case, the expression 10!/(4!5!) doesn’t apply to this particular problem, as it represents a combination rather than the arrangement described. The correct solution is shown in the explanation above, and we’ve double-checked that problem 5 is correct as written.
Thanks again for taking the time to point it out!
Amazing content
It really help a lot to me…keep it up..
I need some solutions for numbers
Exercises 1 to 12 have covered the different types of combinations.
Bravo for the exercises.
Thanksssss