Chapters
Every shape has a centre and a polygon is no exception. The distance from the centre of a polygon to its sides is called apothem. There is no shortcut in finding the apothem. All you need to do is to find the centre of a regular polygon and then draw a line from its centre to the midpoint of one of its sides. That distance is the apothem of that specific polygon. Some apothems are very easy to draw and measurable such as the apothem of a square, sometimes, it becomes difficult like the apothem of a hexagon. If we start talking about apothems of all shapes then it will take years to cover and years for you to understand too. That is why, in this resource, we collected some generic polygons to show you how their apothems are found and calculated.

Apothem of a Square
Square, one of the easiest and generic polygons out in this world. There is almost no complexity with square. All sides are equal and so are the diagonals. Let's find its apothem.
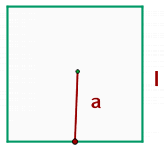
The centre of a square can be found easily by drawing both diagonals and the point where both diagonals intersect is the centre. We draw a line from the centre of the square to its side. We marked the apothem by "a" in the above diagram. Since the centre of a square divides its side into two equal halves, we know that the distance of the apothem will be half of the length of one side.
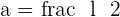
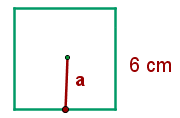
Example
Calculate the apothem of a square with a side of 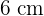 .
.
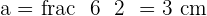
Apothem of a Regular Polygon
Till here, we learned that any shape that has three sides and each side connected are polygons. That means all those geometrical figures that have at least 3 sides are polygon then, what is a regular polygon? It is also a common name given to a pentagon. A pentagon has five sides and each side is connected.
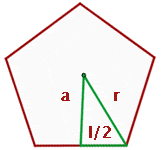
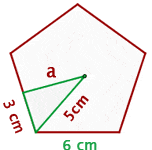
The above diagram shows a regular pentagon, also known as a regular polygon. Let's find its apothem. The centre of a pentagon can be found by drawing diagonals. The point where all diagonals meet each other is the centre of a polygon. Draw a line from the centre of the polygon to any side of the polygon. That is the apothem of a pentagon. However, finding the length of the apothem is a bit tricky. There is no special formula for it, however, we can make our own formula. We can construct a triangle and with the help of that triangle, we use the Pythagorean theorem to find the apothem of the pentagon. By applying the Pythagorean theorem for one of the triangles, we obtain:
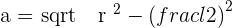
Example
Calculate the apothem of a regular pentagon with a side of 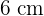 .
.
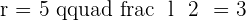
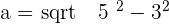
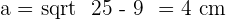
Apothem of a Regular Hexagon
A hexagon is another type of polygon that contains six sides. The word "hex" means five. To find apothem of a regular hexagon, the same concept of apothem of a polygon will be applied. However, there is a small change, the radius of a regular hexagon is the same as the length of a side of a regular hexagon.
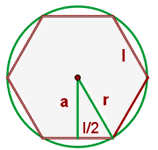
Apply the Pythagorean theorem for the triangle:
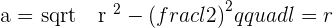
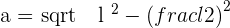
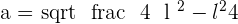
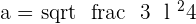
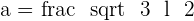
Example
Find the apothem of a regular hexagon inscribed in a circle with a radius of  .
.

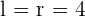
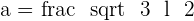
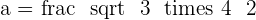














Hi Emma nice to meet u I love reading and solving mathematics problem