What is a 90 Degree Angle
| Definition | Measurement | Notation | |
| Angle | The corner formed by two lines | Degrees |  |
As you can see in the table above, an angle is usually given in degrees. There are many different types of angles that can be formed by two lines. Take a look at some of the common ones below.
| Acute Angle | Obtuse Angle | |
| Degrees | 0-89 | 91-180 |
A 90 degree angle is exactly what it sounds like - it is an angle that equals 90 degrees. It is known as a right angle.
| Right Angle | Notation | |
| Degrees | 90 degrees | Small square |
What are Parallel Lines
Parallel lines are one of the common types of lines. Take a look at the table below for the definition.
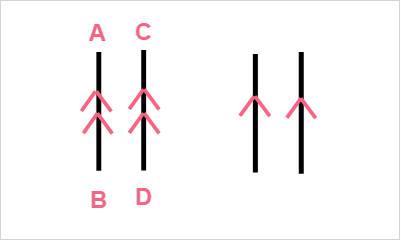
| Definition | Notation | Notation on the line | |
| Parallel Lines | Two lines that never touch and are always the same distance apart |  | Arrows that are the same number |
What are Congruent Lines
In order to understand what congruent lines are, we should specify that we’re really talking about line segments. Take a look at the differences in definitions below.
| Line | Line Segment |
| A straight line that goes to infinity in both directions | A part, or segment, of a line. |
The definition and notation of a line segment is below.
| Definition | Notation | |
| Congruent | Two line segments that have the same length | Matching dashes on the line segments |
We can look at some examples below.
| A | B |
 |  |
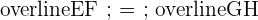Definition of Square
Now that you understand some of these basic concepts, let’s take a look at the definition of a square.
| Definition | |
| Square | A square is a quadrilateral that has four sides that are congruent and has four right angles. |
Let’s take a look at this definition and how the notation on the square looks like.
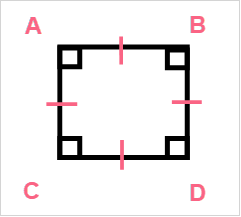
| Property 1 | All touching line segments are perpendicular to each other |
| Property 2 | Opposite line segments are parallel |
Parallelogram
A square is a part of the parallelogram family. Parallelograms are shapes that can be classified by specific properties. Let’s take a look at these properties.
| Property 1 | Is a plane figure, which is a two dimensional figure with no thickness |
| Property 2 | Made up of 3 or more line segments |
| Property 3 | Has four sides |
| Property 4 | Each opposite side is parallel to each other |
| Property 5 | Each opposite side is congruent |
The first 2 properties make up the definition of a polygon, while the combination of the first 3 properties make up the definition of a quadrilateral. There are 3 major types of parallelograms, which you can see in the image below.
| A | B | C |
| Rectangle | Square | Rhombus |
Diagonal of a Square
An additional property of a square can be seen in its diagonal. The diagonal of a square is simply the line that connects each opposite angle. There are two major properties you should know about the diagonal of a square. Take a look at the first one below.
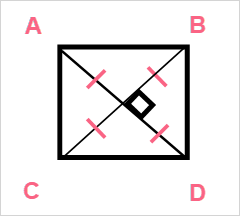
| Description | |
| Diagonal | The two diagonals of a square are perpendicular bisectors |
| Perpendicular bisector | Two lines that are perpendicular at the midpoint of the line |
The second property can be described below in the table.
| Description | |
| Diagonal | The diagonals bisect the angles of each corner |
| Bisecting angles | When angles are cut directly in half |
Perimeter of Square
The perimeter of any shape is the total length of the boundary of the shape. Take a look at an example below.
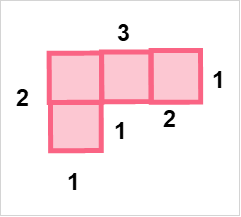
| Notation | Example | |
| Perimeter |  | P = 3+2+1+2+1 |
Since a square has four equal sides (s), the perimeter of a square can be found by either of the following two formulas.
| Equation 1 | Equation 2 | |
| Perimeter | P = s+s+s+s | P = 4*s |
Area of a Square
The area of any shape is the size of the surface contained inside of any boundary. Because you want to be able to compare the areas of all shapes, regardless of what they are, the area is calculated in square units.
| Definition | Use | |
| Square Unit | A square with each side equal to 1 unit | Can compare how many square units are contained in each shape |
The area of a square can be found by simply finding the square of one side. The reason why is explained in the table below.
| A square has four equal sides | Sides equal length of  |
| Square units can be found by multiplying the length times width |  |
| The length and width of a square are equal to each other |  |
| The area is the square of one side |  |
Summarise with AI:
Did you like this article? Rate it!
Loading...
Nice emma really precise information.. I appreciate u
Hey Raptor! Thanks very much for the positive feedback, very much appreciated!
explains everything for a child or a confused student in their ap maths class who is lost in the more detailed mathematics
Draw all types of polygon and its area and perimeter class 7th NCERT course
I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html
Draw all types of polygon and its area and perimeter