Chapters
One of the most important geometrical figures is the triangle. It solves many complex problems in real life. Mathematicians categorized triangles into three types, they are:
- Isosceles triangle
- Equilateral triangle
- Scalene triangle
Each type of triangle has its own properties and these properties should be in detail. That is why we dedicated a single resource for a single type of triangle. This resource will discuss the equilateral triangle.

What is an Equilateral Triangle
The word, "triangle", can be broken into two words, "tri" and "angle", which means a geometrical shape that has three angles. The sum of all angles in a triangle is equal to  . Furthermore, a triangle has three sides. You will find three angles and three sides in every triangle, whether it is isosceles or equilateral.
. Furthermore, a triangle has three sides. You will find three angles and three sides in every triangle, whether it is isosceles or equilateral.
An equilateral triangle has three equal angles and sides. This is the only condition for an equilateral triangle. If one of the sides or angles isn't equal then it won't be an equilateral triangle. Consider the image below:

Check all the sides and angles and check whether you can call it an equilateral triangle or not? If your answer is yes then you are correct! All the angles are the same, 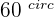 as well as, all the sides are also equal,
as well as, all the sides are also equal,  . Therefore, we can conclude that the above triangle is equilateral.
. Therefore, we can conclude that the above triangle is equilateral.
Perimeter of an equilateral triangle
Perimeter means the sum of all sides. An equilateral triangle has three sides and all sides are equal. Therefore:


Calculate the perimeter of an equilateral triangle with a side of  .
.
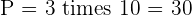
Height of an Equilateral Triangle

To find the height of the triangle, you need to use the Pythagorean theorem. By applying the Pythagorean theorem for one half of the equilateral triangle, we obtain:
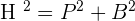
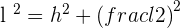
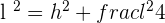

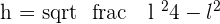

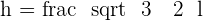
Example
Calculate the height of an equilateral triangle with a side of  .
.

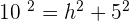
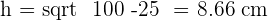
Area of an Equilateral Triangle
The area of triangle is the half of product of base and height. The formula will remain same but since all sides are equal, there will be some modifications in the formula.
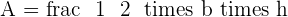
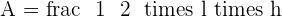
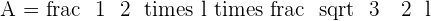
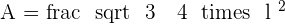
Calculate the area of an equilateral triangle with a side of  .
.

The perimeter of an equilateral triangle measures 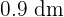 and its height is
and its height is  . Calculate the area of the triangle.
. Calculate the area of the triangle.
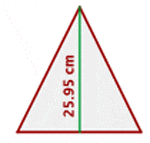
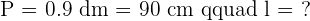
You could find the length either using the height formula or perimeter formula, we will find the length using both formulas:
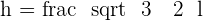

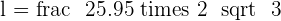
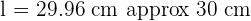

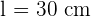
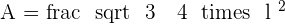
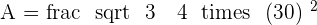
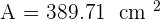
Example
Find the area of the following equilateral triangle:

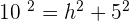
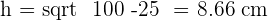

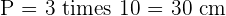
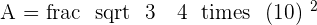
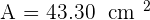
Apothem of an Equilateral Triangle
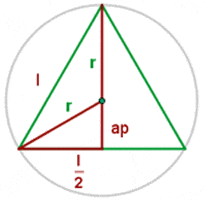
An inscribed triangle means that a triangle that can be easily fitted inside of a circle. The apothem of a triangle is the distance between the center of the triangle and the mid-point of any side of a triangle. To find the apothem of an equilateral triangle, you need to use the Pythagorean theorem. We all know, at this point, that the Pythagorean theorem is used to find the hypotenuse, base (adjacent), and perpendicular (opposite) of a triangle.

The above formula can be used to find the side of an inscribed equilateral triangle. We have the side now, let's find the base (adjacent). An equilateral triangle base is equal to  . Since the apothem divides the base into two equal parts, we can say that the one side will be equal to
. Since the apothem divides the base into two equal parts, we can say that the one side will be equal to  . Once you found the side and the base (adjacent) of an inscribed equilateral triangle, use the Pythagorean theorem to find the apothem.
. Once you found the side and the base (adjacent) of an inscribed equilateral triangle, use the Pythagorean theorem to find the apothem.
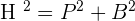
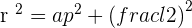
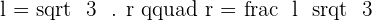


Or, you can use the above formula to find the apothem of an inscribed equilateral triangle.
Example
Calculate the apothem of an equilateral triangle with a side of 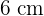 .
.


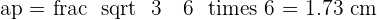
Centroid of an Equilateral Triangle
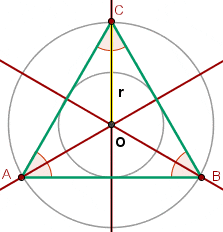
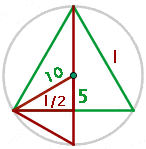
Not only you can find apothem of an equilateral inscribed triangle, but you can find the center of an equilateral inscribed triangle. The center of the circle is the centroid and height coincides with the median. The radius of the circumcircle is equal to two-thirds the height.
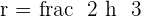
Problems
Calculate the area of an equilateral triangle inscribed in a circle with a radius of 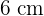 .
.

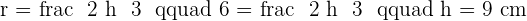
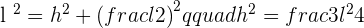


Given an equilateral triangle with a side of 6 cm, find the area of the circular sector determined by the circle circumscribed around the triangle and the radius passing through the vertices.
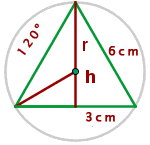
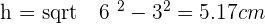
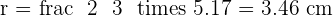

Calculate the side of an equilateral triangle inscribed in a circle of  radius.
radius.
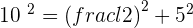














Hi Emma nice to meet u I love reading and solving mathematics problem