It is difficult to solve a three-equation linear system that has three variables. This is because unlike two variable systems, the arithmetic computations in a three equation linear systems are more complex. Solving the complex system of linear equations involving three variables requires a lot of time and effort. Fortunately, we have a Gauss elimination method, that helps us to solve the complex system of linear equations by writing the system of equations in the form of the matrix and applying a series of operations on the matrix to convert it into a reduced row echelon form. Besides solving linear equations, this method can be also used to compute the rank, determinant, and inverse of an invertible square matrix.
"The Gauss elimination method is to transform a system of equations into an equivalent system that is in a triangular form"
To apply row reduction on a matrix, we employ a sequence of elementary row operations to change the matrix in such a way that the new matrix has zeros on the lower left-hand corner. The following three types of elementary row operations are performed on a matrix using the Gauss elimination method:
- Type 1: Two rows are swapped
- Type 2: A row is multiplied by a nonzero number
- Type 3: A multiple of one row is added to another row
By employing the above sequence of operations, a matrix is transformed into an upper triangular matrix that is in a reduced row echelon form. An upper triangular matrix is a square matrix in which all the entries below the main diagonal are zero. A square matrix has an equal number of rows and columns. An example of an upper triangular matrix is given below:

You can see that the above square matrix of the form 3x3 is an upper triangular matrix because all the values below the main diagonal are zeroes. In this matrix, all the leading coefficients are 1 and each column that has the leading coefficient contains zeroes at the other places.
Find out interesting things about a good maths tutor.

What is the Row Echelon Form?
In this article, we have used the word reduced row echelon form. But what does this term actually mean? The answer to this question will be discussed in this section in detail.
The leading coefficient is the leftmost nonzero entry in a matrix in which all the elements in the row are not zeros. The leading coefficient is also known as the pivot of the matrix. Hence, if two leading coefficients are present in the same column, then we apply the row operation of type 3 on the matrix to make one of the coefficients zero. After that, we use the row swapping operation so that the rows can be ordered in such a way that for every non zero rows, the leading coefficient is the right of the leading coefficient in the above row. The matrix in this form is known to be in row echelon form.
Check Superprof for different portfolios of maths tutors.
Example 1
Solve the following system of linear equations:
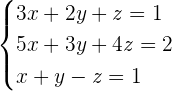
Solution
First, we will write the above system of linear equations in the form of the following matrix:

We will apply the following row operations on the above matrix:


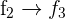

Now, we will apply the following type 3 row operations to the above matrix:
- Subtracting row 2 by three times the value of row 1, i.e.
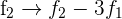
- Subtract row 3 by five times the value of row 1, i.e.
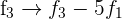

Now, we will subtract row 3 by twice the value of row 2 to convert the matrix into a reduced row echelon form:
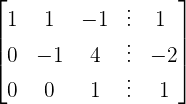
We will write the above matrix in the form of the following system of linear equations:

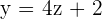
Substitute 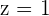
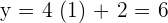

Hence, 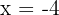 ,
, 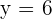 and
and 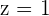
Example 2

Solution
First, we will write the above system of linear equations in a matrix form:

We will apply the type 1 operation by swapping row 2 and 1, i.e. 

Now, we will subtract the 2 times multiple of row 1 from row 2, i.e. 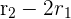 and subtract row 1 from row 3, i.e.
and subtract row 1 from row 3, i.e.  to get the reduced row echelon form:
to get the reduced row echelon form:
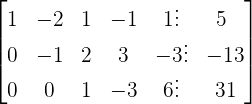
Now, we will write the above matrix in reduced row echelon form in the form of following system of equations:

It is a consistent dependent system. Suppose 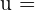 and
and 
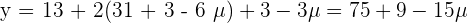
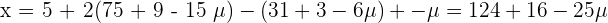
Example 3

Solution
We will write the above system of linear equations in the form of the following matrix:

- We will subtract the 3 times multiple of row 1 from row 2, i.e.
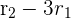
- We will subtract the 5 times multiple of row 1 from row 3, i.e.
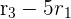
- We will subtract the 2 times multiple of row 1 from row 4, i.e.


Now, we will apply the following row operations on the above matrix:
- Subtract the 7 times multiple of row 3 from row 4, i.e.
 to convert the matrix into a reduced row echelon form:
to convert the matrix into a reduced row echelon form:

As the entire fourth row is zero, therefore it is an inconsistent system.
Example 4

Solution
We will write the above system of linear equations in the form of the matrix form like this:
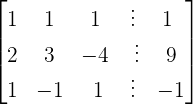
We will apply the following row operations to the above matrix:
- Subtract 2 times multiple of row 1 from row 2, i.e.
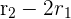
- Subtract row 1 from row 3, i.e.

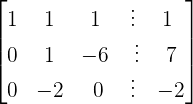


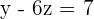
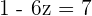
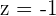
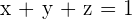
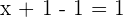

Hence,  ,
,  and
and 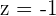 .
.
Example 5
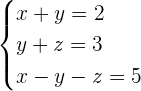
Solution
We will write the above system of linear equations in the form of the matrix form below:

Now, we will subtract the row 1 from row 3, i.e.  :
:
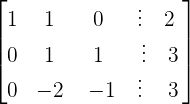
Now, we will add 2 times multiple of row 1 to row 3, i.e. 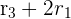 to convert the matrix into a reduced row echelon form:
to convert the matrix into a reduced row echelon form:

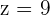
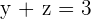





Hence,  ,
,  and
and 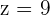 .
.
Find a great maths tutor here.













I am impressed well done.