In the case of a vector, direction is one of the most important components. Without direction, you won't call it a vector, that would be a straight line that has magnitude only. We can find the direction of a vector with the help of cosine. In an orthonormal basis, direction cosines of the vector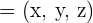

are:

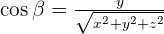
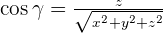
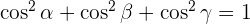
It is necessary that you should be working on an orthonormal basis otherwise this formula won't be valid.

The best Maths tutors available
Poonam
5
5 (80 reviews)
Poonam
£100
/h
Gift icon
1st lesson free!
Paolo
4.9
4.9 (84 reviews)
Paolo
£35
/h
Gift icon
1st lesson free!
Anthony
5
5 (95 reviews)
Anthony
£10
/h
Gift icon
1st lesson free!
Sehaj
4.9
4.9 (62 reviews)
Sehaj
£60
/h
Gift icon
1st lesson free!
Intasar
5
5 (73 reviews)
Intasar
£99
/h
Gift icon
1st lesson free!
Shane
4.9
4.9 (51 reviews)
Shane
£50
/h
Gift icon
1st lesson free!
Tomi
5
5 (40 reviews)
Tomi
£55
/h
Gift icon
1st lesson free!
Hiren
5
5 (34 reviews)
Hiren
£85
/h
Gift icon
1st lesson free!
Poonam
5
5 (80 reviews)
Poonam
£100
/h
Gift icon
1st lesson free!
Paolo
4.9
4.9 (84 reviews)
Paolo
£35
/h
Gift icon
1st lesson free!
Anthony
5
5 (95 reviews)
Anthony
£10
/h
Gift icon
1st lesson free!
Sehaj
4.9
4.9 (62 reviews)
Sehaj
£60
/h
Gift icon
1st lesson free!
Intasar
5
5 (73 reviews)
Intasar
£99
/h
Gift icon
1st lesson free!
Shane
4.9
4.9 (51 reviews)
Shane
£50
/h
Gift icon
1st lesson free!
Tomi
5
5 (40 reviews)
Tomi
£55
/h
Gift icon
1st lesson free!
Hiren
5
5 (34 reviews)
Hiren
£85
/h
Gift icon
1st lesson free!
Let's go

Example

Determine the direction cosines of the vector with components .

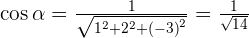
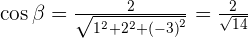
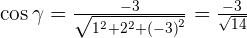
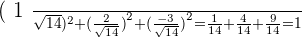
A vector

is drawn on the basis of orthonormal and has components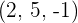

. Find the direction cosines.

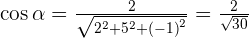
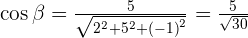
Summarise with AI:

Did you like this article? Rate it!

4.00 (3 rating(s))
Loading...
Emma

Emma

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.