Our whole world is working on the system of coordinates. GPS, locations, and many other things are possible because of coordinates. The idea of coordinates comes from the graph. Without a graphing system, coordinates will not exist. In simple words, the coordinate system is a component of a graph system. You might be wondering why do we need coordinate geometry? The answer is that it connects algebra with geometry. For example, you are asked to find the intersection point of two lines. Your teacher provided both line equations. You can solve it in two ways, either you solve it algebraically i.e. simultaneously or substitution, or you can make your life simple by plotting both lines on the graph. Now you have an idea how coordinate geometry makes algebra more understandable?
Whenever we talk about coordinates, we always specify the type of coordinate system we use. Although there are so many types of coordinates we use today but in this lesson, you will learn the two, most famous, coordinate systems and they are:
- Cartesian Coordinates
- Polar Coordinates

Cartesian Coordinates
Cartesian coordinate system is one of the most used coordinate systems especially in the case of linear motion applications. In fact, you might be familiar with this coordinate system. The cartesian coordinate system defines a point in the form of linear distance from the origin. Although there are three perpendicular axes(x-axis, y-axis, and z-axis), many mathematicians use two perpendicular axes (which are the x-axis, and y-axis). The three axes are used when full precision is required such as finding the location on a map, vectors, etc. These axes are merged to a single point which is known as the "origin". All the axes are also relative to the origin. Origin is the starting point of all axes. This system also allows negative and positive values as well.
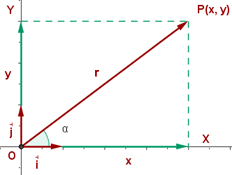
In a system formed by a point, O, and an orthonormal basis at each point, P, there is a corresponds vector, 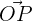 , in the plane such that:
, in the plane such that:

The coefficients x and y of the linear combination are called coordinates of point P.
- The first, x, is the abscissa.
- The second, y, is the ordinate.
As the linear combination is unique, each point corresponds to a pair of numbers and each pair of numbers to a point.
Polar Coordinates
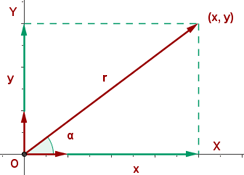
Another mostly used coordinate system is the polar coordinates. Unlike the Cartesian system, polar coordinate system is 2-dimensional. It is mainly used for calculating angles and radius. Polar coordinate system offers you points that are specified by origin (sometimes it can be another reference point, for example, center of rotation) and an angle from a reference direction. The coordinates are in the form of angle and radius  .
.
When the length, r, and the angle, α, (it makes with the x-axis), of the vector are known, the polar coordinates of P are  :
:
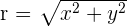


Examples
Convert the following polar coordinates to the cartesian system:
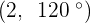
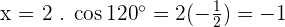

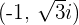



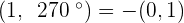
Magnitude
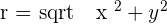
Angle
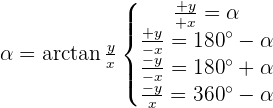
Convert the following cartesian coordinates to the polar system:
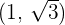



______________________________________________________

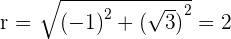
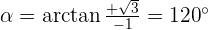
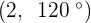
______________________________________________________


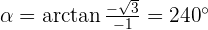
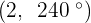
______________________________________________________
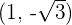
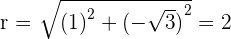
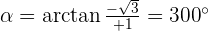

______________________________________________________
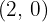

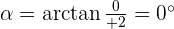
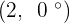
______________________________________________________
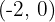
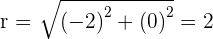
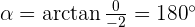
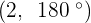
______________________________________________________
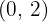
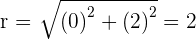
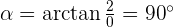
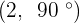
______________________________________________________

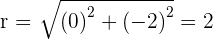

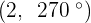
Find various Maths tutors near me on Superprof.













