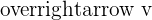Chapters
In this article, we will discuss what are vectors, vector space, and linearly dependent vectors. We will also discuss how to tell whether a given vector set is linearly dependent or not. Before proceeding to discuss the linear dependence of vectors, first, we will define vectors and vector space.

What is a Vector?
A vector refers to a quantity that is described in terms of magnitude, as well as direction. The mathematical notation of a vector is a letter with a right head arrow at the top. For example,
What is Vector space?
"A set of objects also referred to as vectors are known as vector space. Scalar numbers or scalars can be multiplied or added to these vectors. Linear space is another name given to the vector space."
Although, most often, these scalar numbers are real numbers, however, we can multiply vectors with complex or rational numbers. In the next section, we will discuss what is meant by linearly dependent vectors, what are some facts about linearly dependent vectors and their properties.
Linearly Dependent Vectors
A linearly dependent vector can be defined as:
"When at least one of the vectors from a set of vectors can be written as a linear combination of other vectors, then we can say that the vectors are linearly dependent"
Some Facts about Linear Dependence
Some facts about linear dependence are:
- If the two vectors are collinear, then they are linearly dependent. By collinearity, we mean that one of the vectors is a scalar multiple of the other.
- If a set has a zero vector, then it means that the vector set is linearly dependent.
- If the subset of the vector
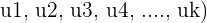 is linearly dependent, then we can say that the vector
is linearly dependent, then we can say that the vector 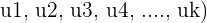 itself is linearly dependent
itself is linearly dependent
The determinant of the linearly dependent matrix is zero. Mathematically we can write it as:

Properties of Linearly Dependent Vectors
Let us summarize the properties of linearly dependent vectors.
- If many vectors are linearly dependent, then at least one of them can be described as a linear combination of other vectors.
- If a vector in a vector set is expressed as a linear combination of others, all the vectors in that set are linearly dependent.
- The linearly dependent vectors are parallel to each other.
- If the components of any two vectors
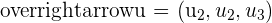 and
and 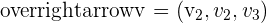 are proportional, then these vectors are linearly dependent.
are proportional, then these vectors are linearly dependent.
Example 1
Determine the values of k for the linearly dependent vectors  ,
,  and
and 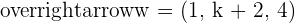 .
.
Solution
We know that the vectors are linearly dependent if the determinant of the matrix is zero, meaning that the rank of the matrix is less than 3.

Recall the formula of finding the determinant of a 3x3 matrix and use it to find the determinant of the above matrix:
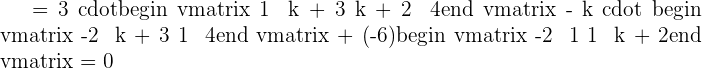

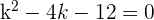

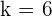
Example 2
Determine whether the following vectors are linearly dependent or independent.

Solution
In the first step of solving this problem, we will multiply the vectors u, v and w with a, b and c respectively in such a way that a + b + c = 0
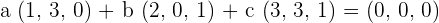
Write the above equation as system of equation like this:

Now, we will write the equation is matrix form to find the determinant:

Recall the formula for finding the determinant of the 3 x 3 matrix and utilize it to compute the determinant of the matrix form of above equation:
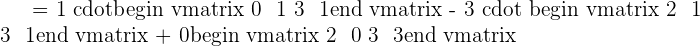
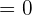
The zero determinant shows that the vectors are linearly dependent.
Example 3
Determine the values of t for the linearly dependent vectors  ,
,  and
and 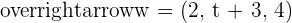 .
.
Solution
If the determinant of the matrix is zero, then vectors are linearly dependent. It also means that the rank of the matrix is less than 3. Hence, write the vectors in matrix form and set the matrix equal to zero like this:

Recall the formula of finding the determinant of a 3x3 matrix and use it to find the determinant of the above matrix:
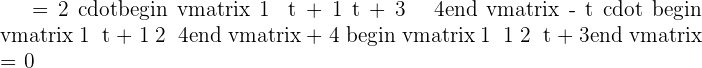


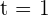
Hence, for t = 1 the vectors will be linearly dependent vectors.
Example 4
Determine the values of s for the linearly dependent vectors 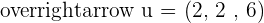 ,
, 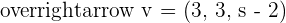 and
and 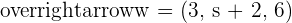 .
.
Solution
If the determinant of the matrix is zero, then vectors are linearly dependent. It also means that the rank of the matrix is less than 3.
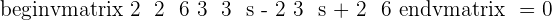
Recall the formula of finding the determinant of a 3x3 matrix and use it to find the determinant of the above matrix:

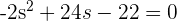
Divide both sides by -2 to get the following equation:

Solve the above equation by factoring:
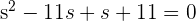

Set each factor equal to zero:
 and
and 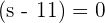
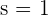 and
and 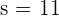
Hence, for s is equal to 1 and 11 the set of vectors are linearly dependent.
Example 5
Determine the values of x for the linearly dependent vectors  ,
, 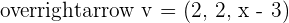 and
and 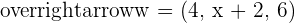 .
.
Solution
If the determinant of the matrix is zero, then vectors are linearly dependent. It also means that the rank of the matrix is less than 3. Hence, for this reason, we will write the vectors in matrix form and set it equal to zero.
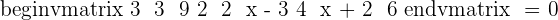
Recall the formula of finding the determinant of a 3x3 matrix and use it to find the determinant of the above matrix:
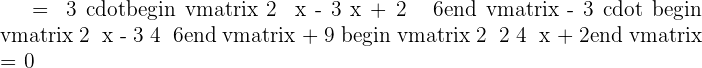

Divide both sides by -3 to get the following equation:
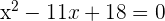
Solve the above equation by factoring:
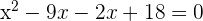

Set each factor equal to zero:
 and
and 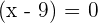
 and
and 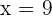
Hence, for x is equal to 2 and 9 the set of vectors are linearly dependent.
Find various Maths teacher on Superprof.