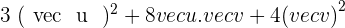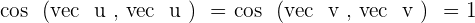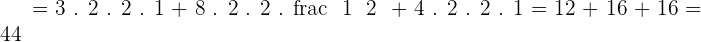At this point, you might have an understanding of vectors, the importance of vectors, and why we use them in our daily life? Let's have a small recap, a vector is a line that has a direction and magnitude. Both properties define a vector. It means that changing one property changes the whole vector. Few applications of vectors are calculation of velocity, newton's law of fluid mechanics, GPS, aerodynamics, and many more.
Let's say you have two vectors, your teacher asks you to combine both vectors. Now, what would you do? Add them? Adding them doesn't mean combine, for that we use a fundamental way which is known as the dot product. Another name of the dot product is the scalar product. So, what is a dot product? Dot product tells us the quantity of one vector from the second vector's direction perspective. In easy words, it tells how much one vector is in amount but in the direction of the second vector. Furthermore, it also combines two vectors, it joins the tail of one vector to the tail of the second vector. In addition, you also find how much your first vector deviates from the second vector.
The scalar product or dot product of two vectors  and
and 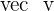 is equal to:
is equal to:
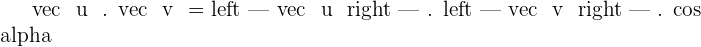
Where,
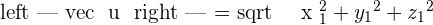

In some text books, dot product formula might be written as:
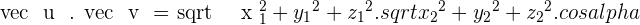
Both are same formulas and will gave you the same result. The only difference between both formulas is that the first formula, the magnitude of both vectors  are written in magnitude form. You need to calculate the magnitude of both vectors separately and then use it in that formula. On the other hand, the second formula has magnitude formula infused. In simple words, you don't need extra effort, just replace all the variables with their values and that is it!
are written in magnitude form. You need to calculate the magnitude of both vectors separately and then use it in that formula. On the other hand, the second formula has magnitude formula infused. In simple words, you don't need extra effort, just replace all the variables with their values and that is it!
One of the keen interest points of the dot product is the angle between both vectors. Many researchers are only concern with the degree of deviation. The angle part of the dot product is defined by the 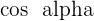 . If both vectors are perpendicular to each other, the dot product will be equal to zero. No matter how big the magnitude of the vector is, if both vectors are perpendicular to each other, it will always result in zero. This is because
. If both vectors are perpendicular to each other, the dot product will be equal to zero. No matter how big the magnitude of the vector is, if both vectors are perpendicular to each other, it will always result in zero. This is because 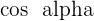 is zero at
is zero at 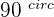 . However, if both vectors are opposite to each other, it will always result in a negative number because
. However, if both vectors are opposite to each other, it will always result in a negative number because  is equal to
is equal to  . Last but not least, if the angle between both vectors is zero then the dot product will be maximum and why is it? Because
. Last but not least, if the angle between both vectors is zero then the dot product will be maximum and why is it? Because  is equal to
is equal to 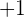 .
.
Find more Maths tutor here on Superprof.

Example

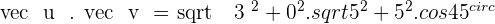

It can also be expressed as:
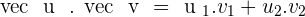
Example
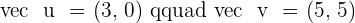

Magnitude of a Vector
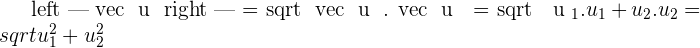
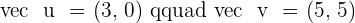
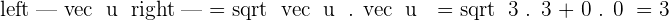
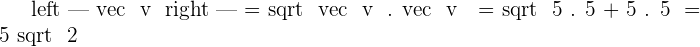
Properties of Dot Product
Commutative
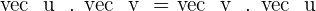
Associative

Distributive

The dot product of a non-zero vector is always positive
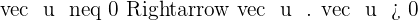
Example
Calculate the scalar product of the following vectors:
1. 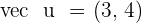 and
and 
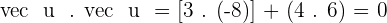
2. 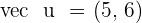 and
and 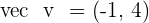
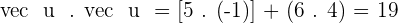
3.  and
and 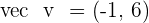

___________________________________________________________________
If 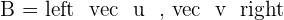 is a basis of vectors in the plane, such that
is a basis of vectors in the plane, such that 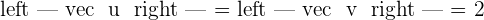 and
and 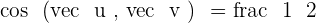 and:
and:
 and
and 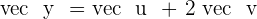
Calculate  .
.

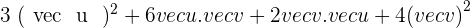
The scalar product is commutative.