Chapters
Vectors are mathematical tools used to describe quantities that have both magnitude (size) and direction — such as velocity, force, or displacement. Unlike regular numbers (scalars), vectors point somewhere and can exist in two or three dimensions.
In this guide, we’ll break down the most important vector formulas used in maths and physics. You’ll learn:
- How to write a vector in component form
- How to calculate magnitude and direction
- How to use dot and cross products
- Where these formulas are used in real-world applications
Whether you’re revising for exams or brushing up on your vector knowledge, this article will help you understand not just the formulas — but how and why they work.
| Formula | Purpose | Output |
|---|---|---|
| v = xi + yj + zk | Express vector components | Vector |
| |v| = √(x² + y² + z²) | Find vector magnitude | Scalar |
| u = v / |v| | Get unit vector | Vector |
| a + b | Add vectors | Vector |
| a · b | Dot product (angle, projection) | Scalar |
| a × b | Cross product (perpendicular vector) | Vector |
| AB = b - a | Displacement vector | Vector |
| cos(θ) = (a · b)/|a||b| | Angle between vectors | Scalar (angle) |
The best Maths tutors available
Sehaj
£60
/h
1st lesson free!
Intasar
£129
/h
1st lesson free!
Johann
£50
/h
1st lesson free!
Hiren
£149
/h
1st lesson free!
Poonam
£100
/h
1st lesson free!
Harjinder
£25
/h
1st lesson free!
Syed
£50
/h
1st lesson free!
Farooq
£50
/h
1st lesson free!
Sehaj
£60
/h
1st lesson free!
Intasar
£129
/h
1st lesson free!
Johann
£50
/h
1st lesson free!
Hiren
£149
/h
1st lesson free!
Poonam
£100
/h
1st lesson free!
Harjinder
£25
/h
1st lesson free!
Syed
£50
/h
1st lesson free!
Farooq
£50
/h
1st lesson free!
🔺 Basic Vector Notation
Components
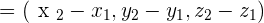
Magnitude or Length
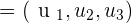
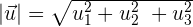
🔹Vector Notation Formula
v = xi + yj + zk
Explanation:
This is the standard way to write a vector in 2D or 3D. The vector is broken down into its component parts along the x, y, and z axes. The values of x, y, and z are the magnitudes in each direction. The letters i, j, and k represent unit vectors in the x, y, and z directions, respectively.
This is the standard way to write a vector in 2D or 3D. The vector is broken down into its component parts along the x, y, and z axes. The values of x, y, and z are the magnitudes in each direction. The letters i, j, and k represent unit vectors in the x, y, and z directions, respectively.
Used when:
You need to represent a direction and magnitude in space.
You need to represent a direction and magnitude in space.
Why it's useful:
This form makes it easy to add, subtract, or manipulate vectors algebraically and visually.
This form makes it easy to add, subtract, or manipulate vectors algebraically and visually.
🔹Magnitude (Length) of a Vector
|v| = √(x² + y² + z²)
Explanation:
This formula calculates the length or size of a vector using Pythagoras' Theorem. It applies to 2D and 3D vectors.
This formula calculates the length or size of a vector using Pythagoras' Theorem. It applies to 2D and 3D vectors.
Used when:
You want to know how long a vector is — for example, the distance between two points.
You want to know how long a vector is — for example, the distance between two points.
Why it's useful:
It gives a scalar value (just a number) that tells you how strong or far the vector goes, which is key in physics (like speed, force).
It gives a scalar value (just a number) that tells you how strong or far the vector goes, which is key in physics (like speed, force).
🔹Unit Vector Formula
Explanation:
A unit vector has a magnitude of 1 but still points in the same direction as the original vector. This formula scales the vector down to unit length.
A unit vector has a magnitude of 1 but still points in the same direction as the original vector. This formula scales the vector down to unit length.
Used when:
You need to keep the direction of a vector but remove its magnitude — often in physics or directional problems.
You need to keep the direction of a vector but remove its magnitude — often in physics or directional problems.
Why it's useful:
Unit vectors are essential for defining direction without affecting calculations involving magnitude (like direction of force or velocity).
Unit vectors are essential for defining direction without affecting calculations involving magnitude (like direction of force or velocity).
🔹Vector Addition
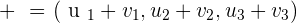
Explanation:
To add two vectors, you add their corresponding components. So x-components add to x, y to y, and so on.
To add two vectors, you add their corresponding components. So x-components add to x, y to y, and so on.
Used when:
Two or more forces/movements act on a body and you want the net effect.
Two or more forces/movements act on a body and you want the net effect.
Why it's useful:
Helps combine movements or forces into a single result — e.g. in navigation, motion, or engineering.
Helps combine movements or forces into a single result — e.g. in navigation, motion, or engineering.
🔹 Dot Product (Scalar Product)
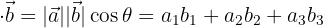
Explanation:
This formula gives a scalar (number) that represents how much one vector goes in the direction of another. It can be found either using the angle between them or by multiplying matching components.
This formula gives a scalar (number) that represents how much one vector goes in the direction of another. It can be found either using the angle between them or by multiplying matching components.
Used when:
You want to know the angle between vectors, check if they’re perpendicular (dot product = 0), or find work done (in physics).
You want to know the angle between vectors, check if they’re perpendicular (dot product = 0), or find work done (in physics).
Why it's useful:
Helps combine movements or forces into a single result — e.g. in navigation, motion, or engineering.
Helps combine movements or forces into a single result — e.g. in navigation, motion, or engineering.
🔹Cross Product (Vector Product)
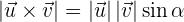
Explanation:
This formula gives a new vector that is perpendicular to both original vectors. It involves direction and magnitude.
This formula gives a new vector that is perpendicular to both original vectors. It involves direction and magnitude.
Used when:
You need to find a vector perpendicular to a plane defined by two other vectors — e.g. torque, angular momentum, surface normals.
You need to find a vector perpendicular to a plane defined by two other vectors — e.g. torque, angular momentum, surface normals.
Why it's useful:
Vital in 3D applications, physics, and engineering. The result’s direction follows the right-hand rule.
Vital in 3D applications, physics, and engineering. The result’s direction follows the right-hand rule.
🔹 Displacement Vector (Between Two Points)
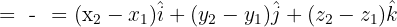
Explanation:
This formula finds the vector from point A to point B by subtracting the coordinates of A from B.
This formula finds the vector from point A to point B by subtracting the coordinates of A from B.
Used when:
You’re finding direction and distance between two locations in space.
You’re finding direction and distance between two locations in space.
Why it's useful:
It gives both the path and direction of motion, helpful in physics, navigation, and kinematics.
It gives both the path and direction of motion, helpful in physics, navigation, and kinematics.
🔹Angle Between Two Vectors
Explanation:
This rearranges the dot product formula to solve for the angle between two vectors.
This rearranges the dot product formula to solve for the angle between two vectors.
Used when:
You need to measure the angle of separation or alignment between two directions.
You need to measure the angle of separation or alignment between two directions.
Why it's useful:
Determines whether vectors are perpendicular, parallel, or at another angle — crucial in geometry and physics.
Determines whether vectors are perpendicular, parallel, or at another angle — crucial in geometry and physics.
📐 More Complex Vector Formulas
Linearly Dependent Vectors
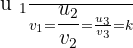
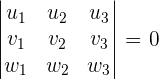
Linear Independent Vectors
Magnitude of a Vector
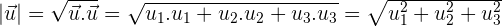
Orthogonal Vectors
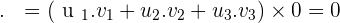
Direction Cosine
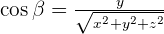
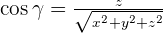
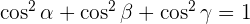
Orthogonal Vectors
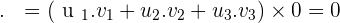
Direction Cosine
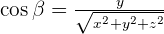
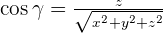
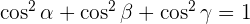
Cross Product
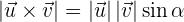
Area of a Parallelogram
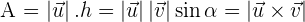
Area of a Triangle
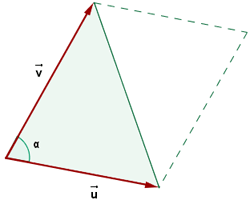
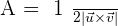
Scalar Triple Product
Volume of a Parallelepiped
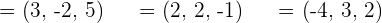
Volume of a tetrahedron
Did you like this article? Rate it!
Loading...
