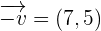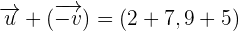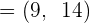Chapters
In this article, we will discuss how to add and subtract vectors. But before proceeding to discuss the addition and subtraction of vectors, first, let us define vectors.
A vector refers to a quantity that is described by magnitude, as well as direction. It is depicted by an alphabet with a right head arrow on the top. For instance,
and
etc are used to represent vectors.
In other words, we can say that the vectors refer to the geometric representations of the magnitude and direction. The magnitude and direction are depicted by straight arrows, that start from one point on a coordinate axis and culminate at a different point. The magnitude of the vectors is actually their length. This length represents some value so that the vector is comparable to another vector. The arrows of the vectors show that they have a direction. This is the primary difference between scalar and vector as scalars are quantities without direction.

Key Points to Remember for Vectors
Some of the key points, that you should remember for vectors are:
- The two components of a vectors are the magnitude and its direction.
- The examples of vectors in real life include acceleration, distance, force, and speed because these terms are described by both the magnitude and direction.
- We define vectors not only by their magnitude but also by their orientation corresponding to a set of coordinates.
- When we try to analyze vectors, then we often break them down into different parts or components. For vectors that are two-dimensional, these parts are horizontal and vertical. On the other hand, for three dimensional vectors, the magnitude part is same, however, we depict the direction part in terms of x, y, and z.
Adding two vectors
For the addition of two vectors,  and
and  , you should join the tail of the one vector with the head of the other vector as shown in the figure below.
, you should join the tail of the one vector with the head of the other vector as shown in the figure below.

 in the above figure and it is equal to the distance from the tail of the first vector
in the above figure and it is equal to the distance from the tail of the first vector 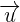 to the head of the second vector
to the head of the second vector  .
. Parallelogram Rule
You can also employ a parallelogram rule to add vectors. To do so, draw the vectors in such a way that their tails (initial points) coincide with each other. After that, you should sketch the lines to complete a parallelogram. The diagonal which extends from the initial point to the opposite vertex of the parallelogram is the result of this addition.
This rule is depicted in the figure below.
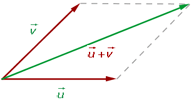
You can see that the tails of the vectors  and
and  coincide with each other. Then from the heads of both the vectors, we have sketched the lines to get a parallelogram. In the end, we sketched a diagonal from the initial point to the opposite vertex that is depicted by the green colored line. This diagonal is the result of the addition and is mathematically represented as
coincide with each other. Then from the heads of both the vectors, we have sketched the lines to get a parallelogram. In the end, we sketched a diagonal from the initial point to the opposite vertex that is depicted by the green colored line. This diagonal is the result of the addition and is mathematically represented as  .
.
If you are given two vectors 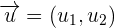 and
and 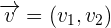 , then how will you add these vectors?
, then how will you add these vectors?
Well, the addition is simple. All you have to do is to add the components of the vectors like this:

Properties of Vector Addition
Some properties of vector addition are given below:
Associative property
The associative property of vector addition is mathematically notated as:
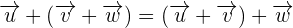
Commutative property
The commutative property of vector addition is mathematically represented as:
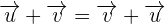
Additive property
According to additive property of vector addition, if zero vector is added to a vector then the result is the vector itself:
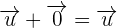
Additive inverse or opposite property
The additive inverse or opposite property of vectors say that:
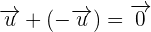
Subtracting Vectors
Now, that you know how to add two vectors, you may be wondering how to subtract two vectors because addition and subtraction of vectors are closely related. Only the sign between the components is changed. A depiction of subtraction through a triangle is shown in the figure below:
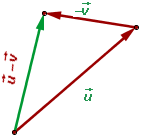
 and
and  , you need to add the vector
, you need to add the vector  with the opposite of the vector
with the opposite of the vector 
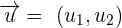
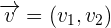

Example 1
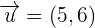 and
and 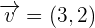 then find
then find 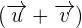 and
and 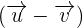 .
.Solution
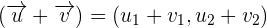


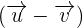 . For this, we will rewrite
. For this, we will rewrite 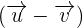 as
as 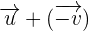
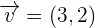 , then
, then 
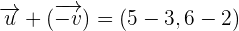

Example 2
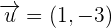 and
and  then find
then find 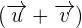 and
and 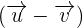 .
.Solution
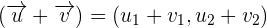

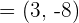
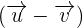 . For this, we will rewrite
. For this, we will rewrite 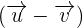 as
as 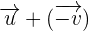
 , then
, then 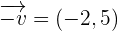
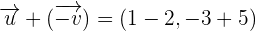

Example 3
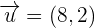 and
and  then find
then find 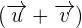 and
and 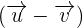 .
.Solution
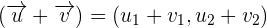

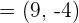
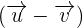 . For this, we will rewrite
. For this, we will rewrite 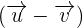 as
as 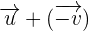
 , then
, then 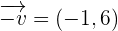
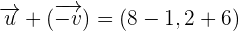
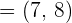
Example 4
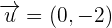 and
and 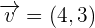 then find
then find 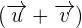 and
and 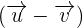 .
.Solution
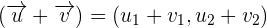
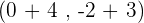

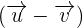 . For this, we will rewrite
. For this, we will rewrite 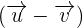 as
as 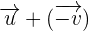
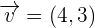 , then
, then 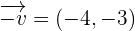
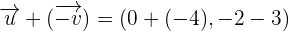
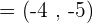
Example 5
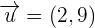 and
and  then find
then find 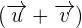 and
and 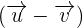 .
.Solution
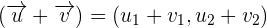


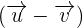 . For this, we will rewrite
. For this, we will rewrite 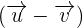 as
as 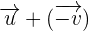
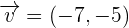 , then
, then