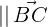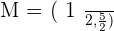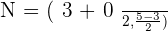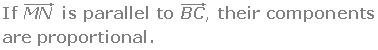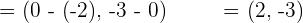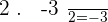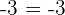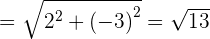Vectors don't need to be a single entity. It can be created by different vectors as well. However, one of the biggest concerns of mathematicians is that whether the vectors can be linearly dependent or not? It is very important since it shows the relationship of vectors. Many students think that only linear dependence matters but, in fact, linear independence matters a lot as well. It has its own importance. One of its biggest application is in research work and computer languages. In this lesson, you will learn all the fundamentals of linear dependence and independence.

Linear Combination
Suppose you have three vectors,  , and
, and  . Although, these vectors have different points but there might be a linear combination between them. If we add
. Although, these vectors have different points but there might be a linear combination between them. If we add  and
and  then we observed that the answer is equal to vector
then we observed that the answer is equal to vector  .
.

Hence, we can conclude that  . It means that vector
. It means that vector  and
and  have a linear combination. Furthermore, they are linearly dependent as well but we will talk about it later in this resource. If you change any element of any vector, it will cause changes in other vectors. In nutshell, given the numbers
have a linear combination. Furthermore, they are linearly dependent as well but we will talk about it later in this resource. If you change any element of any vector, it will cause changes in other vectors. In nutshell, given the numbers  and the vectors
and the vectors  , a linear combination is each of the vectors of the form:
, a linear combination is each of the vectors of the form:

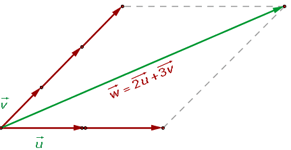
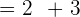
Given the vectors 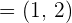 and
and  , calculate the linear combination vector
, calculate the linear combination vector 

Can the vector  be expressed as a linear combination of the vectors
be expressed as a linear combination of the vectors  and
and  ?
?
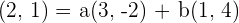

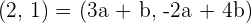
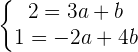
After solving the above equations simultaneously, we will get:
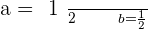
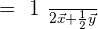
Linearly Dependent Vectors
Vectors are linearly dependent if there is a linear combination of them that equals the zero vector, without the coefficients of the linear combination being zero.
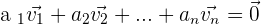
Properties
1.If several vectors are linearly dependent, then at least one of them can be expressed as a linear combination of the others.


If a vector is a linear combination of others, then all the vectors are linearly dependent.
2.Two vectors in the plane are linearly dependent if, and only if they are parallel.
3.Two vectors in the plane  and
and 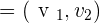 are linearly dependent if their components are proportional.
are linearly dependent if their components are proportional.

Find various Maths tutors near me on Superprof.
Linearly Independent Vectors
Several vectors are linearly independent if none of them can be expressed as a linear combination of the others. For example, there are three vectors, they are not scalar multiples of each other neither any relation was observed by performing mathematical operations. It means that all three vectors are lineraly independent vectors. In nutshell, they will have no relation with each.
Determine if the vectors are linearly dependent or independent:
 and
and 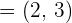

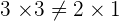
Hence, both vectors are Linearly independent
Determine if the vectors are linearly dependent or independent:
 and
and 

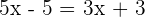

Are vectors are linearly dependent for  .
.
Determine if the vectors are linearly dependent or independent:
 and
and 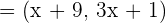
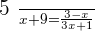


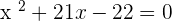

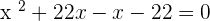




They are linearly dependent for  and
and 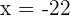
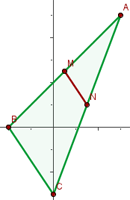
Check that the line segment joining the midpoints of sides AB and AC of the triangle: 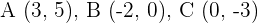 are parallel to the side BC and equal to its half.
are parallel to the side BC and equal to its half.