Exercise 1
Calculate the head of the vector 
knowing that its components are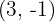 
and its tail is 
.
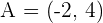Exercise 2
Given points 
and 
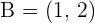, calculate the value of a if the magnitude of the vector is one.
Exercise 3
Normalize the vectors: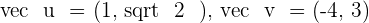 
and 
.
Exercise 4
Determine the unit vector, 
, which is in the same direction as the vector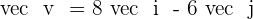 
.
Exercise 5
Calculate the coordinates of D so that the quadrilateral formed by the vertices: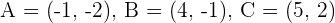 
and D; is a parallelogram.
Exercise 6
The vectors 
and 
form a basis. Express this in basis the vector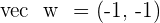 
.
Exercise 7
Find the value of k so that the angle that forms between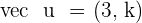 
and 
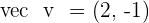is:
1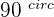 
2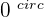 
3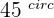 
Exercise 8
Calculate the value of a so that the vectors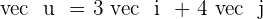 
and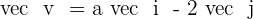 
form an angle of .
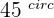Exercise 9
If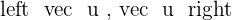 
is an orthonormal basis, calculate:
1 
2 
3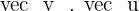 
4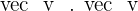 
Solution of exercise 1
Calculate the head of the vector knowing that its components are 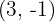and its tail is .
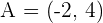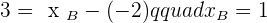
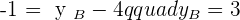
Solution of exercise 2
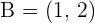Given points and , calculate the value of a if the magnitude of the vector is one.
Solution of exercise 3
Normalize the vectors: 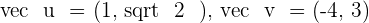and .
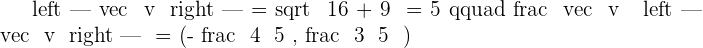
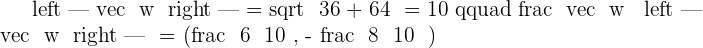
Solution of exercise 4
Determine the unit vector, , which is in the same direction as the vector .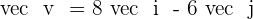
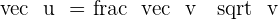
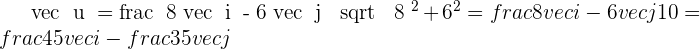
Solution of exercise 5
Calculate the coordinates of D so that the quadrilateral formed by the vertices: 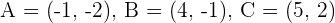and D; is a parallelogram.
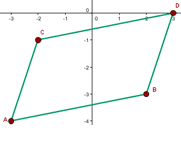
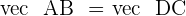
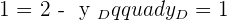
Hence,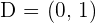 
Solution of exercise 6
The vectors and form a basis. Express this in basis the vector .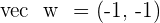
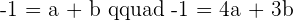
Replacing the value of a in the second equation:
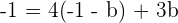
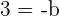
Plugging the value of b in the first equation:
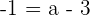
Solution of exercise 7
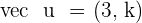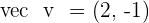Find the value of k so that the angle that forms between and is:
1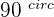
2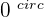
3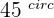
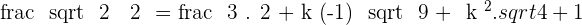
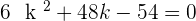
After solving the above equation:
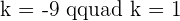
Solution of exercise 8
Calculate the value of a so that the vectors 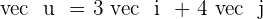and 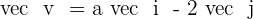form an angle of .
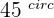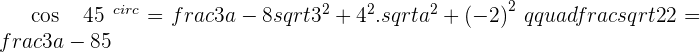
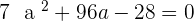
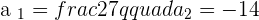
Solution of exercise 9
If 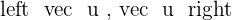is an orthonormal basis, calculate:
1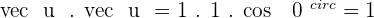 
2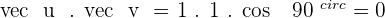 
3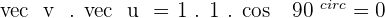 
4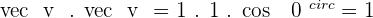 
Find more Maths tutors here on Superprof.
Summarise with AI:
Did you like this article? Rate it!
Loading...
