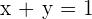Relation Between Linear Algebra and Linear Combination of Vectors
The world of linear algebra is vast. There are so many things that the more you learn the more you figure out that you know nothing. For this lecture, let's just stick to linear algebra combination. Linear combination means combining two or more two algebraic parts to make it one.
(scalar quantity)(variable 1) + (scalar quantity)(variable 2) + (scalar quantity)(variable 1) ... (scalar quantity)(variable n)
A scalar quantity usually represents numbers because numbers depend on quantity not direction and that is why they are scalar quantity. The scalar quantity is multiplied with the variable (which is our main focus). There is no term limit applied when performing linear combinations. The result will be in the form of the variable. The question is that whether vectors work the same as an algebraic linear combination? The answer is yes! A linear combination of two or more vectors is the vector obtained by adding two or more vectors (with different directions) which are multiplied by scalar values.



The above equation shows that the vector  is formed when two times vector
is formed when two times vector  is added to three times the vector
is added to three times the vector  . The scalar quantity matters a lot, it won't change the resulting consequence but it will surely change the resulting quantity. For example,
. The scalar quantity matters a lot, it won't change the resulting consequence but it will surely change the resulting quantity. For example,  , it means if we add
, it means if we add  , it will give us a unit vector
, it will give us a unit vector  , what if we change the scalar quantity of both parent vectors? It won't give us the unit vector
, what if we change the scalar quantity of both parent vectors? It won't give us the unit vector  .
.
Find various Maths teacher on Superprof.
Example
Write the vector  as a linear combination of the vectors:
as a linear combination of the vectors:  .
.


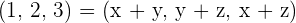
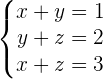


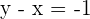
Adding the first equation and the last equation:
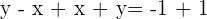


Replacing the value of y in the second equation:
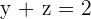
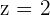
Replacing the value of y in the first equation: