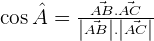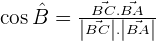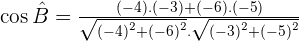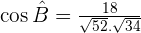Whenever you dot product two vectors, it will always create an angle. In a few cases, we multiply vectors with each other without an angle because both vectors are in the same direction. Remember, directions in vectors are very important, what if both vectors have different directions? Then they will always create an angle which we can find from the dot product of vectors. To find the angle, we use  and then we multiply it with the magnitudes of both vectors to find the dot product but in this lesson, you are not here to learn the dot product, you are here to find how to find the angle between two vectors.
and then we multiply it with the magnitudes of both vectors to find the dot product but in this lesson, you are not here to learn the dot product, you are here to find how to find the angle between two vectors.

Finding the Angle Through Dot Product
Below is the formula to find the dot product of any two vectors in a 2 dimension:
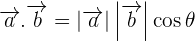
Now, let's turn this equation in terms of angle. The 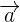 and
and 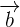 represents vector "a" and "b". Since we are talking about 2 dimensions here, both vectors will have 2 points, one on the x-axis and other on the y-axis. These vectors are written in form of this:
represents vector "a" and "b". Since we are talking about 2 dimensions here, both vectors will have 2 points, one on the x-axis and other on the y-axis. These vectors are written in form of this:

and when you multiply both vectors they will result in: 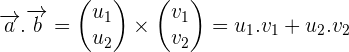
Let's solve for their magnitudes in form of u and v:

Since we have all the values now, let's insert them in the original equation (which is the dot product equation):
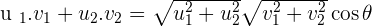
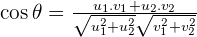
The above equation is the final equation to find the angle between two vectors. All you need to do is to insert the values of 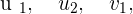 and
and 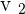 in the equation and whatever results, don't forget to find the cos inverse value of the answer to get the angles in degrees. For more clarification, we have a couple of examples which will help you to understand better.
in the equation and whatever results, don't forget to find the cos inverse value of the answer to get the angles in degrees. For more clarification, we have a couple of examples which will help you to understand better.
Examples




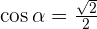
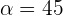
Calculate the dot product and the angle formed by the following vectors:
1. 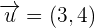 and
and 

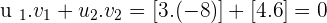



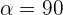
2. 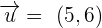 and
and 

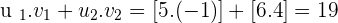

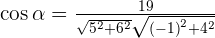
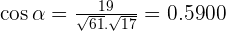

3. 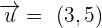 and
and 



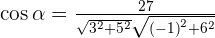
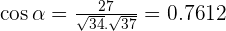
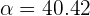
Given the vectors  and
and 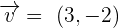 , calculate the value of k so that the vectors
, calculate the value of k so that the vectors 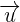 and
and  are:
are:
1 Perpendicular.


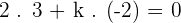
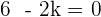
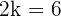

2 Parallel.


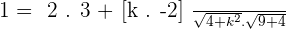
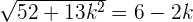
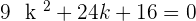
Factorizing the above equation:
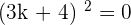


3 Make an angle of  °.
°.
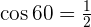
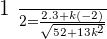
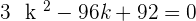
After breaking the middle term and solving for k:
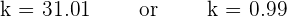
Find various Maths tutor near me on Superprof.
Find the value of k if the angle between  and
and 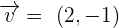 is:
is:
 °
°


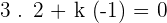

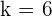
 °
°


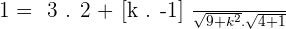
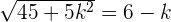
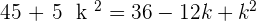

After breaking the middle term, the answer of k will be:

 °
°
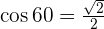
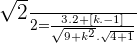
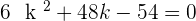
After solving the middle term equation, the values of k will be:

Calculate the angles of the triangle with vertices:  and
and  .
.