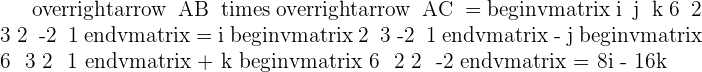Exercise 1
Find two unit vectors for
and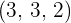
and determine the orthogonal vector for the two.
Exercise 2
Find a unit vector that is perpendicular to
and
.
Exercise 3
Given the vectors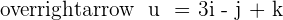
and
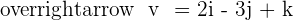, find the product
and verify that this vector is orthogonal to
and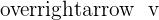
. Also, find the vector
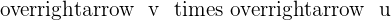and compare it with
.
Exercise 4
Consider the following figure:
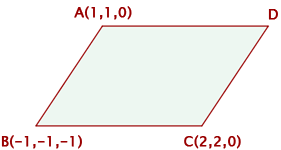
Determine:
1 The coordinates of D if ABCD is a parallelogram.
2 The area of the parallelogram.
Exercise 5
Given the points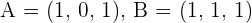
and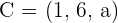
, determine:
1 What values of a are collinear.
2 Determine if values exist for a so that A, B, and C are three vertices of a parallelogram of area 
. If values do exist, determine the coordinates of C:
Exercise 6
and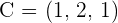
are the three vertices of a triangle.
1. Calculate the cosine of each of the three angles in the triangle.
2. Calculate the area of the triangle.
Solution of exercise 1
Find two unit vectors for and 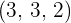and determine the orthogonal vector for the two.
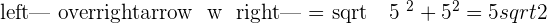
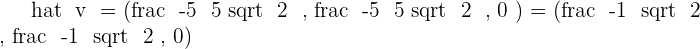
Solution of exercise 2
Find a unit vector that is perpendicular to and .
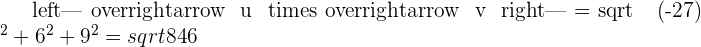
Solution of exercise 3
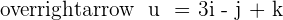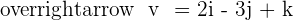Given the vectors and , find the product and verify that this vector is orthogonal to and 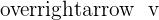. Also, find the vector 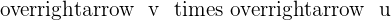and compare it with .
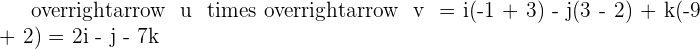
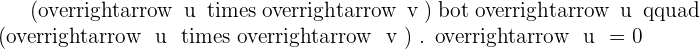
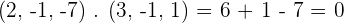
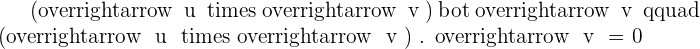
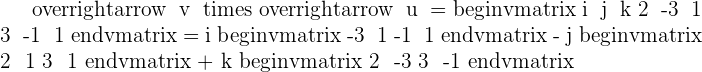
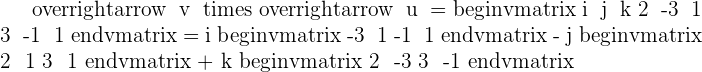
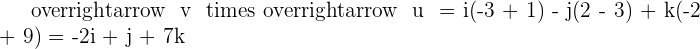
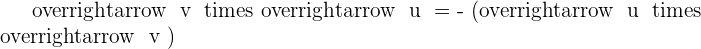
Solution of exercise 4
Consider the following figure:
Determine:
1 The coordinates of D if ABCD is a parallelogram.
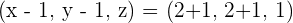
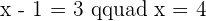
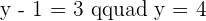
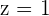
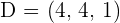
2 The area of the parallelogram.
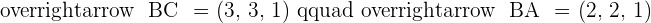
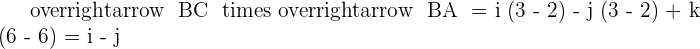
Solution of exercise 5
Given the points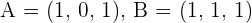
and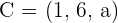
, determine:
1 What values of a are collinear.
If A, B, and C are collinear, the vectors 
and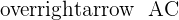 
are linearly dependent and have proportional components.
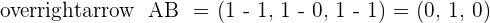
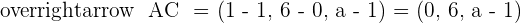
2 Determine if values exist for a so that A, B, and C are three vertices of a parallelogram of area . If values do exist, determine the coordinates of C:
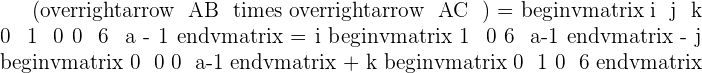
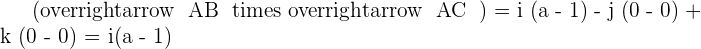
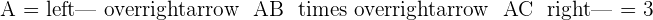
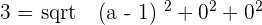
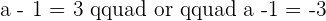
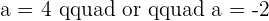
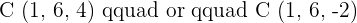
Find various Maths tutors near me on Superprof.
Solution of exercise 6
and
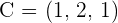are the three vertices of a triangle.
1. Calculate the cosine of each of the three angles in the triangle.
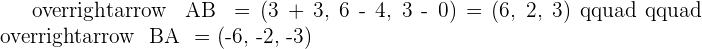
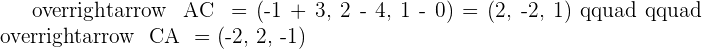
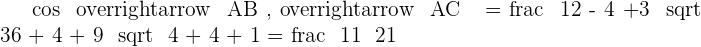
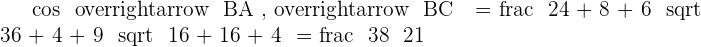
2. Calculate the area of the triangle.
Summarise with AI:
Did you like this article? Rate it!
Loading...
