Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 1 Solution
- Exercise 2 Solution
- Exercise 3 Solution
- Exercise 4 Solution
- Exercise 5 Solution
- Exercise 6 Solution
- Exercise 7 Solution
- Exercise 8 Solution
- Exercise 9 Solution
- Exercise 10 Solution
- Exercise 11 Solution
- Exercise 12 Solution
- Exercise 13 Solution
- Exercise 14 Solution
- Exercise 15 Solution
- Exercise 16 Solution

Exercise 1
Determine the fraction that matches the description below:
a. half of a half
b. half of a third
c. a third of a half
d. half of a quarter
Exercise 2
To prepare a cake, you need:
 of a package of
of a package of 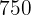 g of sugar
g of sugar
 of a
of a  kg package of flour
kg package of flour
 of a bar of butter of weighing
of a bar of butter of weighing  g
g
Find the quantities that are needed to prepare the cake in grams.
Exercise 3
A well contains  liters of water. If
liters of water. If  of its original content is consumed, how many liters of water are left in the well?
of its original content is consumed, how many liters of water are left in the well?
Exercise 4
A piece of cloth measuring  m in length is cut to
m in length is cut to  of its original length. What is the length of the piece that has been removed?
of its original length. What is the length of the piece that has been removed?
Exercise 5
A family consumed the following amounts of liquids during their Saturday picnic:
Two bottles of water each measuring a liter and a half
 bottles of juice each measuring
bottles of juice each measuring  of a liter
of a liter
 bottles of lemonade each measuring
bottles of lemonade each measuring  of a liter
of a liter
How many liters of liquid did the family drink during their picnic? Express the result using a mixed number.
Exercise 6
How many thirds of a liter are there in  liters?
liters?
Exercise 7
A cable measuring  m is cut into two pieces. One piece of the cable is
m is cut into two pieces. One piece of the cable is 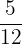 of the original length. What is the length of each piece of cable?
of the original length. What is the length of each piece of cable?
Exercise 8
A box contains  chocolates. Eva ate
chocolates. Eva ate  of the chocolates and Ana ate
of the chocolates and Ana ate  of the chocolates.
of the chocolates.
a. How many chocolates did Eva eat?
b. How many chocolates did Ana eat?
c. What fraction of the  chocolates have been eaten so far?
chocolates have been eaten so far?
Exercise 9
Adriana has walked  m on her way to school. This distance is
m on her way to school. This distance is  of the total distance from her house to the school. What is the total distance from her house to the school?
of the total distance from her house to the school. What is the total distance from her house to the school?
Exercise 10
Two cars A and B are making the same journey of  km. At a particular moment, Car A has traveled
km. At a particular moment, Car A has traveled 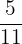 of the trip, while car B has traveled
of the trip, while car B has traveled 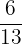 of it.
of it.
a. If the cars continue at the same speed, which of the two will arrive at the destination first?
b. How many kilometers had each car driven at that particular moment?
Exercise 11
After the ballots have been counted in a city's local election, it was determined that 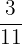 of the votes went to Party A,
of the votes went to Party A, 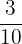 went to Party B,
went to Party B, 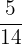 went to Party C and the remainder went to Party D. The total number of votes was
went to Party C and the remainder went to Party D. The total number of votes was  .
.
Calculate:
a. The number of votes obtained by each party.
b. The number of registered voters who did not cast a ballot if the total amount of voters that did was  of the total amount of voters who are registered.
of the total amount of voters who are registered.
Exercise 12
Helen went to the women's boutique starting out with 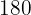 dollars. She spent
dollars. She spent  of that amount on new clothes. How much money does Helen have left?
of that amount on new clothes. How much money does Helen have left?
Exercise 13
A few years ago Peter was  , which represents
, which represents  of the amount of his current age. How old is Peter now?
of the amount of his current age. How old is Peter now?
Exercise 14
A father has divided up  dollars among his 3 sons. The eldest son received
dollars among his 3 sons. The eldest son received  of the whole amount, while the middle son received
of the whole amount, while the middle son received  and the youngest son received the remainder.
and the youngest son received the remainder.
a. How much money did each sibling receive?
b. What fraction of the money did the youngest son receive?
Exercise 15
The budget for a residential complex is distributed as follows:  th for electricity,
th for electricity,  th for water,
th for water, 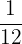 th for garbage collection,
th for garbage collection,  th for building maintenance and the remainder is reserved for cleaning the complex.
th for building maintenance and the remainder is reserved for cleaning the complex.
a. What fraction of the budget is used for cleaning?
b. Order the expenses from least to greatest.
Exercise 16
Alicia had  dollars to go shopping with. Thursday she spent
dollars to go shopping with. Thursday she spent  of that amount and Saturday she spent
of that amount and Saturday she spent  of what she had left.
of what she had left.
a. How much money did she spend each day?
b. How much money does she have left at the end?
Exercise 1 Solution
Determine the fraction that matches the description below:
a. half a half
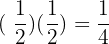
b. half of a third
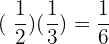
c. a third of a half
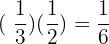
d. half of a quarter
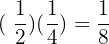
Exercise 2 Solution
To prepare a cake, you need:
 of a package of
of a package of 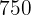 g of sugar
g of sugar
 of a
of a  kg package of flour
kg package of flour
 of a bar of butter of
of a bar of butter of 
Find the quantities that are needed to prepare the cake in grams.
 of
of 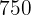 g is
g is 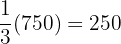 g of sugar
g of sugar
 of
of  g is
g is 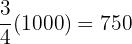 g of flour
g of flour
 of
of  g is
g is 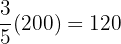 g of butter
g of butter
Exercise 3 Solution
A well contains  liters of water. If
liters of water. If  of its original content is consumed, how many liters of water are left in the well?
of its original content is consumed, how many liters of water are left in the well?
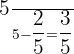 is the fractional amount left in the well.
is the fractional amount left in the well.
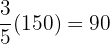 liters is the amount of water left in the well.
liters is the amount of water left in the well.
Exercise 4 Solution
A piece of cloth measuring  m in length is cut to
m in length is cut to  of its original length. What is the length of the piece that has been removed?
of its original length. What is the length of the piece that has been removed?
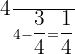 is the fractional amount of the piece that was removed.
is the fractional amount of the piece that was removed.
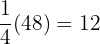 m is the length of the piece that was removed.
m is the length of the piece that was removed.
Exercise 5 Solution
A family consumed the following amounts of liquids during their Saturday picnic:
Two bottles of water each measuring a liter and a half
 bottles of juice each measuring
bottles of juice each measuring  of a liter
of a liter
 bottles of lemonade each measuring
bottles of lemonade each measuring  of a liter
of a liter
How many liters of liquid did the family drink during their picnic? Express the result using a mixed number.
amount of water drank: 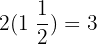 liters
liters
amount of juice drank: 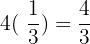 liters
liters
amount of lemonade drank: 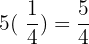 liters
liters
total amount of liquids drank: 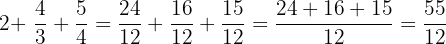 liters
liters
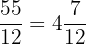 liters
liters
Exercise 6 Solution
How many thirds of a liter are there in  liters?
liters?
There are three  liters in
liters in 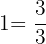 liter.
liter.
There are 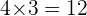 thirds
thirds  's of a liter in
's of a liter in  liters.
liters.
Exercise 7 Solution
A cable measuring  m is cut into two pieces. One piece of the cable is
m is cut into two pieces. One piece of the cable is 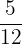 of the original length. What is the length of each piece of cable?
of the original length. What is the length of each piece of cable?
The fractional length of the second piece of cable: 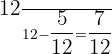 .
.
The 2 pieces are 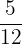 th and
th and 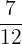 th of the original length.
th of the original length.
The length of the first piece: 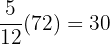 m.
m.
The length of the second piece: 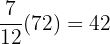 m.
m.
Exercise 8 Solution
A box contains  chocolates. Eva ate
chocolates. Eva ate  of the chocolates and Ana ate
of the chocolates and Ana ate  of the chocolates.
of the chocolates.
a. How many chocolates did Eva eat?
Eva ate 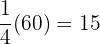 chocolates.
chocolates.
b. How many did Ana eat?.
Ana ate 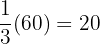 chocolates
chocolates
c. What fraction of the total amount of chocolates has been eaten between them?
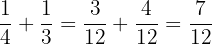
Exercise 9 Solution
Adriana has walked  m on her way to school. This distance is
m on her way to school. This distance is  th of the total distance from her house to the school. What is the total distance from her house to the school?
th of the total distance from her house to the school. What is the total distance from her house to the school?
 of the total distance plus
of the total distance plus  of the total distance will be the actual total distance.
of the total distance will be the actual total distance.
 is
is  of
of 
Find  of the distance
of the distance  m.
m.
 of
of  m is
m is  m
m
The total distance is  m.
m.
Exercise 10 Solution
Two cars A and B make the same journey of  km. At a particular moment, Car A has traveled
km. At a particular moment, Car A has traveled 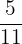 of the trip, while Car B has traveled
of the trip, while Car B has traveled 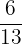 of it.
of it.
a. If the cars continue at the same speed, which of the two will arrive at the destination first?
Car A has traveled 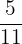 of the total trip and car B has traveled
of the total trip and car B has traveled 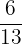 of the total trip.
of the total trip.
Car A: 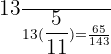 of the trip
of the trip
Car B: 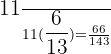 of the trip
of the trip
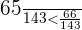 so Car B will make it to the end of the journey just a hair faster than Car A.
so Car B will make it to the end of the journey just a hair faster than Car A.
b. How many kilometers have been traveled at this particular moment by each car?
Car A: 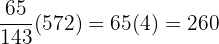 km
km
Car B: 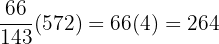 km
km
Exercise 11 Solution
After the ballots have been counted in a city's local election, it was determined that 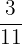 th of the votes went to Party A,
th of the votes went to Party A, 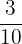 th went to Party B,
th went to Party B, 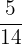 th went to Party C and the remainder went to Party D. The total number of votes was
th went to Party C and the remainder went to Party D. The total number of votes was  .
.
Calculate:
a. The number of votes obtained by each party.
Party A has 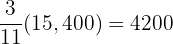 votes
votes
Party B has 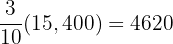 votes
votes
Party C has 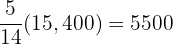 votes
votes
Party D has 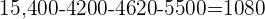 votes
votes
b. The number of registered voters who did not cast a ballot if the number of voters who did was  of the total amount of voters who are registered.
of the total amount of voters who are registered.
 of the total amount of registered voters is
of the total amount of registered voters is  voters,
voters,
so  of the total amount of people who voted,
of the total amount of people who voted,  , will be
, will be  of the total amount of registered voters.
of the total amount of registered voters.
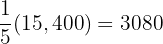 is
is  of the registered voters,
of the registered voters,
so  is the total amount of registered voters.
is the total amount of registered voters.
Exercise 12 Solution
Helen went to the women's boutique starting out with 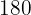 dollars. She spent
dollars. She spent  of that amount. How much money does she have left?
of that amount. How much money does she have left?
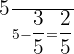
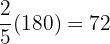 dollars
dollars
Exercise 13 Solution
A few years ago Peter was 24, which represents  of his current age. How old is Peter now?
of his current age. How old is Peter now?
 of Peter's current age plus
of Peter's current age plus  of Peter's current age will be Peter's actual current age.
of Peter's current age will be Peter's actual current age.
 is
is  of
of 
 of
of  is
is 
present age is 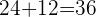
Exercise 14 Solution
A father has divided up  dollars among his 3 sons. The eldest son received
dollars among his 3 sons. The eldest son received  of the whole amount, while the middle son received
of the whole amount, while the middle son received  and the youngest son received the remainder.
and the youngest son received the remainder.
a. How much money did each sibling receive?
The eldest son received 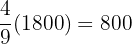 dollars.
dollars.
The middle son received 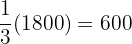 dollars.
dollars.
The youngest son received 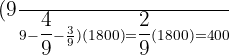 dollars.
dollars.
b. What fraction of the money was the amount given to the youngest son?
The youngest son received  of the original amount.
of the original amount.
Exercise 15 Solution
The budget for a residential complex is distributed as follows:  th for electricity,
th for electricity,  th for water,
th for water, 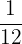 th for garbage collection,
th for garbage collection,  th for building maintenance and the remainder is reserved for cleaning the complex.
th for building maintenance and the remainder is reserved for cleaning the complex.
a. What fraction of the budget is used for cleaning?
Budget without cleaning expenses: 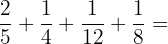
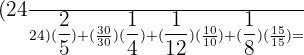
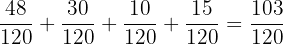
Cleaning expenses: 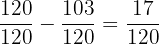
b. Order the expenses from least to greatest.
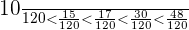
garbage 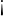 maintenance
maintenance 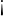 cleaning
cleaning 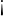 water
water 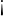 electricity
electricity
Exercise 16 Solution
Alicia had  dollars to go shopping. Thursday she spent
dollars to go shopping. Thursday she spent  th of that amount and Saturday she spent
th of that amount and Saturday she spent  th of what she had left.
th of what she had left.
a. How much money did she spend each day?
Thursday Alicia spent 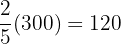 dollars.
dollars.
She has 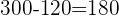 dollars left for more shopping.
dollars left for more shopping.
Saturday Alicia spent 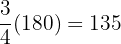 dollars.
dollars.
b. How much does she have left at the end?
She has  dollars left.
dollars left.
Summarise with AI:












