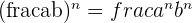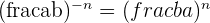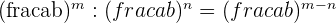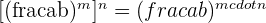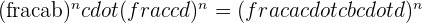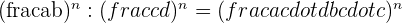Chapters
In this resource, we have compiled all the concepts of a fraction and the relevant formulas. Before proceeding to discuss them, first, let us recall what is a fraction and its types.

Introduction
A fraction depicts parts of a whole or a collection. It is composed of two numbers, a numerator, and the denominator. The number above the line is known as the numerator and the number below the line is called the denominator.
We can have the fraction of a whole or fraction of a set/collection. The fraction of a whole is used when a thing is divided into equal parts and we have to represent each part as a fraction of a whole. For instance, if a cake is divided into eight equal parts, then each part is represented by the fraction 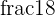 .
.
The fraction of a collection shows the number of elements from the given set or collection. For example, Sarah had 20 cookies. She gave 11 to her friend Mariah, 5 to her younger brother John and 4 to her younger sister, Alice. The number of cookies each person gets is represented by the fractions in the following way:
Number of cookies Mariah gets = 
Number of cookies John gets gets = 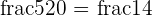
Number of cookies Alice gets = 
You should keep the following things in mind while solving fractions:
- The denominator of the fraction cannot be zero.
- If the numerator of the fraction is 0, then the fraction is equal to 0.
- A whole number or constant has 1 in the denominator. In other words, if we have a fraction that has 1 in its denominator, then the fraction is equal to the numerator.
Types of Fractions
There are three types of fractions:
- Proper Fractions: The fractions in which the numerator is less than the denominator are known as proper fractions. For example,
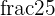 ,
,  , and
, and 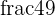 are proper fractions.
are proper fractions. - Improper Fractions: The fraction in which the numerator is greater than the denominator is called an improper fraction. For example,
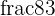 ,
, 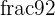 , and
, and 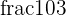 are improper fractions.
are improper fractions. - Mixed Fraction: These fractions have two parts - an integer or a whole number part and a fractional part.
Mixed fractions can be converted into improper fractions and vice versa.
Fractions Formulas
Now, let us discuss some of the formulas that are useful in solving fractions
Converting Mixed Fraction to Improper Fractions
As we have discussed above, we can convert mixed fractions to improper fractions. All we have to do is to multiply the denominator of the fractional part with the whole number or integer and add the numerator to it. The number we obtain after applying these series of arithmetic operations of multiplication and addition will be written in the numerator. The denominator will remain as it is.
We have translated the above method in the following formula:
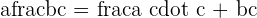
Example
Convert 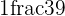 into an improper fraction.
into an improper fraction.
Solution
The numerator is 3, the denominator is 9, and the whole number is 1. Now, we will put these values in the following formula to get the improper fraction:
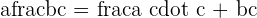


Equivalent Fractions
Two fractions are equivalent if and only if the product of the numerator of one fraction and the denominator of other fraction is equal to the product of the numerator of one and the denominator of other fraction. Mathematically, we can write it as:
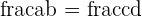 if
if 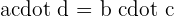
Adding and Subtracting Fractions
With the Same Denominator
The arithmetic operations of addition, subtraction, multiplication, and division can be applied on fractions. We often have two kinds of fractions in the problems, the fractions having the same denominator and the fractions with different denominators. The arithmetic operations of addition and subtraction of both types of fractional problems require different procedures.
When in a problem, we are given the fractions with the same denominator, then we simply add or subtract the numerators of the fractions and keep the denominator as it is. Mathematically, it is written as:
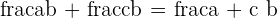

Example
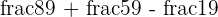
Solution
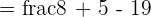
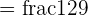
As both the numerator and denominator are multiples of a common number 3, therefore we can simplify the above fraction like this:

With a Different Denominator
The procedure for solving the fractions having different denominators is different. We need to convert these types of fractions into the fractions with same denominator by using the common denominator method or by taking the LCM. LCM stands for Least Common Denominator and is also known as LCD (Least Common Divisor).
Common Denominator Method
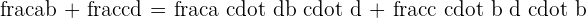

Example
Solve 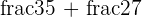 using the common denominator method.
using the common denominator method.
Solution
We will multiply the denominator of one fraction with the numerator and the denominator of other fraction to make the denominators equal.
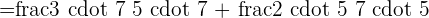
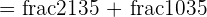
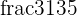
Least Common Denominator Method
To use this method, find LCM of the denominators. LCM is the smallest number that can be evenly divided by both the denominators. After taking LCM, divide each denominator by the LCM and take the product of the dividend and the numerator. Repeat this process for both the fractions.

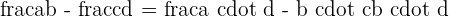
Example
Using the LCM method, solve the following fractions:
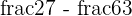
Solution
The smallest number that can be evenly divided by 3 and 7 is 21.
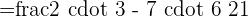
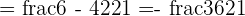
The fraction can be simplified further because 36 and 21 are multiples of 3.

Multiplying Fractions
Multiplying fractions is simple. All you need to do is to take the product of numerators and denominators separately. Mathematically it is written as:

Example
Solve 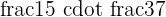
Solution
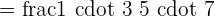
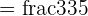
Dividing Fractions
To divide the fractions, take the reciprocal of the second fraction and replace the sign of the division with multiplication simultaneously. Taking reciprocal means inverting fractions, so that the numerator becomes the denominator and denominators becomes the numerator. Mathematically, it is written as:
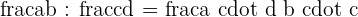
Example
Solve 
Solution
We will take the reciprocal of the second fraction and replace the division sign by multiplication like this:


Powers
The formulae for the powers of fractions are given below: