Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12

Exercise 1
Associate the following fractions with the corresponding amount of minutes in an hour:
 ,
,  ,
,  ,
, 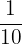 ,
, 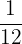 ,
, 
Exercise 2
Find the pairs of equivalent fractions and place them in pairs:
 ,
,  ,
,  ,
, 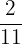 ,
, 
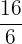 ,
, 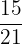 ,
, 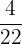 ,
,  ,
, 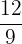
Exercise 3
Write the reciprocals of the following fractions:
 ,
,  ,
, 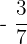 , 5,
, 5, 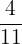 ,
, 
Exercise 4
Write the sign > or <, to create a correct statement.
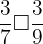 ,
, 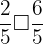 ,
, 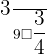 ,
, 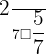
Exercise 5
Write the sign > or <, to create a correct statement.
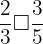 ,
, 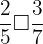 ,
, 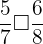 ,
, 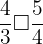
Exercise 6
Order the following fractions from smallest to largest:
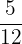 ,
, 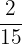 ,
,  ,
, 
Exercise 7
Classify the following fractions as either proper or improper fraction:
 ,
,  ,
,  ,
,  ,
,  ,
, 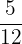 ,
,  ,
, 
Exercise 8
Solve:
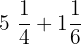
Exercise 9
Solve using two different methods:
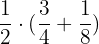
Exercise 10
Solve:
1. 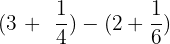
2. 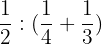
3. 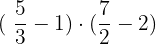
4. 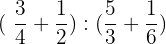
Exercise 11
Solve:
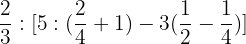
Exercise 12
Perform the divisions:
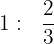

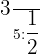
Solution of exercise 1
Associate the following fractions with the corresponding amount of minutes in an hour:
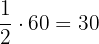 minutes
minutes
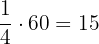 minutes
minutes
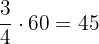 minutes
minutes
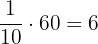 minutes
minutes
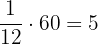 minutes
minutes
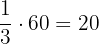 minutes
minutes
Solution of exercise 2
Find the pairs of equivalent fractions and place them in pairs:
 ,
,  ,
,  ,
, 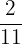 ,
, 
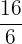 ,
, 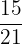 ,
, 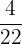 ,
,  ,
, 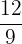
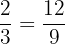

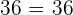
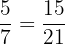
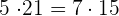
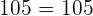
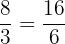


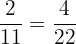
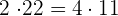
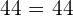
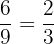
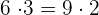
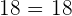
Solution of exercise 3
Write the reciprocals of the following fractions:
 ,
,  ,
, 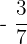 , 5,
, 5, 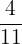 ,
, 
 ,
,  ,
, 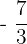 ,
,  ,
, 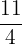 , 8
, 8
Solution of exercise 4
Write the sign > or <, to create a correct statement.
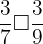 ,
, 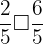 ,
, 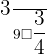 ,
, 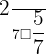
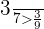 ,
, 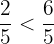 ,
, 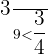 ,
, 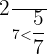
Solution of exercise 5
Write the sign > or <, to create a correct statement.
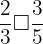 ,
, 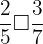 ,
, 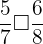 ,
, 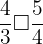
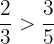 ,
, 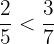 ,
, 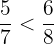 ,
, 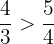
Solution of exercise 6
Order the following fractions from smallest to largest:
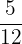 ,
, 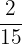 ,
,  ,
, 
We will make the denominators same by multiplying every fraction by a constant.
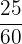 ,
, 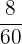 ,
, 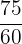 ,
, 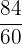
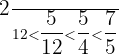
Solution of exercise 7
Classify the following fractions as either proper or improper:
 ,
,  ,
,  ,
,  ,
,  ,
, 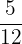 ,
,  ,
, 
Proper:  ,
,  ,
,  ,
, 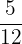 ,
, 
Improper:  ,
,  ,
, 
Solution of exercise 8
Solve:
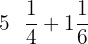
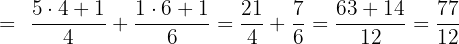
Solution of exercise 9
Solve using two different methods:
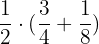
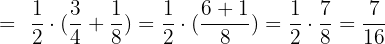
Solution of exercise 10
Solve:
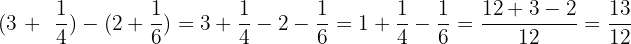
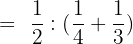
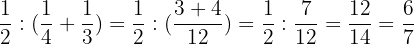
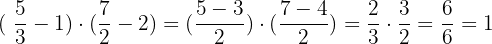
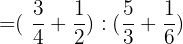
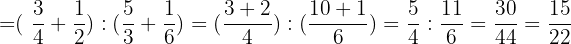
Solution of exercise 11
Solve:
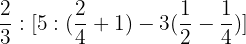
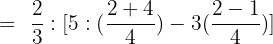
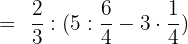
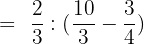
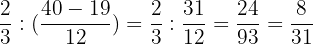
Solution of exercise 12
Perform the divisions:
1 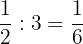
2 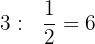
3 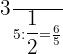
Summarise with AI:












