Chapters
You already know how to add, subtract, multiply, and divide numbers. A fraction is different from the number as it has two numbers, a numerator, and a denominator. A numerator is a number at the top of the fraction and a denominator is a number below the numerator.
The numerator generally describes how many pieces or parts of something you have. A denominator represents the total number of parts.
Consider the following scenario:
Sarah baked 10 cookies on the weekend. She takes 6 of them and gives the remaining cookies to her friend. How will you write this in the form of a fraction?
Since the total cookies are 10, therefore we will write 10 in the denominator.
Fraction of cookies Sarah have = 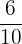
A fraction of cookies Sarah's friend have = 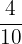
Important Points to Consider While Solving Fractions
When solving fractions, you should keep the following points in mind:
- A fraction having a zero numerator is equal to zero. For example, the fractions
 ,
,  , and
, and  are equal to 0 because they have 0 in their numerators.
are equal to 0 because they have 0 in their numerators. - We cannot divide a fraction by zero. It means that it is impossible to have zero in the denominator of a fraction.
- A fraction having the same numerator and denominator is equal to 1. For example,
 and
and  are equal to 1.
are equal to 1. - The denominators of whole numbers and constants are 1. For example, we assume that the denominators of the whole numbers 10, 12, 8, 6, and 5 are 1.

Types of Fractions
A fraction has the following three types:
- Proper Fractions: In these types of fractions, the numerator is smaller than the denominator. For example,
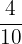 ,
,  , and
, and  are proper fractions because of the numerators smaller than the denominators.
are proper fractions because of the numerators smaller than the denominators. - Improper Fractions: In these fractions, the numerator is greater than the denominator. For example, the fractions
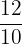 ,
, 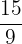 , and
, and  are improper fractions because of the numerators greater than the denominators.
are improper fractions because of the numerators greater than the denominators. - Mixed Fractions: These fractions are written by combining a whole number and the fraction. For example,
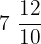 ,
, 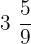 , and
, and 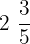 are mixed fractions because they are written by combining the whole numbers and fractions.
are mixed fractions because they are written by combining the whole numbers and fractions.
Converting Fractions From One Form to Another
We can convert an improper fraction to a mixed fraction and vice versa. To convert an improper fraction to a mixed fraction, simply divide the numerator by the denominator. Write the quotient at the whole number place and the remainder as a numerator of the fraction part of the mixed fraction. The denominator will remain the same.
For example, convert the improper fraction  into a mixed fraction.
into a mixed fraction.
First, we will divide 7 by 5. By doing so, we will get the quotient 1 and remainder 2. The denominator will be the same. Hence, 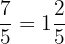 .
.
We can also convert a mixed fraction to an improper fraction. We do so by multiplying the denominator with the whole number part of the fraction and adding a numerator to it. The resulting number we get after multiplication and addition is written in the numerator and the denominator remains the same.
Suppose you are asked to convert 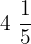 into an improper fraction. First, we will multiply the denominator 5 with the whole number 4 to get 20. Lastly, we will add the numerator 1 to it to obtain the number 21. The denominator will remain the same and we will write 21 in the numerator. Hence, we can say that
into an improper fraction. First, we will multiply the denominator 5 with the whole number 4 to get 20. Lastly, we will add the numerator 1 to it to obtain the number 21. The denominator will remain the same and we will write 21 in the numerator. Hence, we can say that 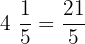 .
.
How to Subtract Fractions?
Now, you know a fraction and its types, let us see how to subtract two fractions. While adding and subtracting fractions, you will come across two kinds of fractions:
- Fractions with the same denominators
- Fractions with different denominators
We will explain how to subtract the two types of fractions one by one.
Subtracting Fractions with the Same Denominator
The fractions which have the same denominators, but different numerators can be subtracted easily. To do so, we just keep the denominator as it is and subtract the numerators. For example, 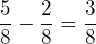 .
.
Subtracting Fractions with a Different Denominator
We follow a procedure to add or subtract fractions that have different denominators. To do so, we find L.C.M (Least Common Multiple) of the two numbers. The least common multiple also known as lowest common multiple or least common divisor is the smallest number that can be evenly divisible by the two numbers. For instance, the L.C.M of (5, 2) is 10 because 10 is the smallest number that can be easily divisible by the two numbers 5 and 2. Similarly, the L.C.M of (2, 6) is 6 because 6 is the smallest number that can be easily divisible by both numbers 2 and 6.
After taking the L.C.M, we write it in the denominator. For the numerator, we divide the denominator of each fraction by the L.C.M and multiply the quotient obtained after dividing by the numerators of each fraction.
Consider the following example:
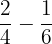
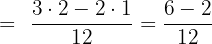
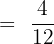
Since, both the numerator and denominator are multiples of 4, therefore we will reduce the above fraction in simplified form:
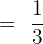
Example 1
Subtract 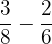
Solution
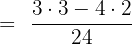
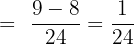
Example 2
Subtract 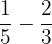
Solution
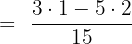
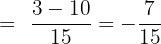
Example 3
Subtract 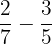
Solution
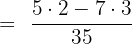
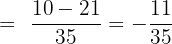
Example 4
Subtract 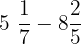
Solution
The above fractions are written in the form of mixed fractions, therefore, to subtract them we will convert them into improper fractions.
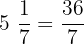
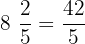
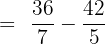
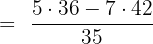
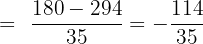
In the next examples, we will see how to solve fractions word problems.
Example 5
Alice has  kg of sugar. She uses
kg of sugar. She uses  kg of sugar to bake a cake. How much sugar is left?
kg of sugar to bake a cake. How much sugar is left?
Solution
Total sugar = 
Sugar used in baking a cake = 
Sugar left = 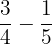
= 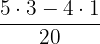
= 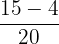
=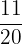
Hence, 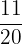 kg of sugar is left.
kg of sugar is left.
Example 6
George spends  of an hour to complete a math exercise. His friend Harry takes
of an hour to complete a math exercise. His friend Harry takes  an hour to complete the same exercise. How much more time (in fraction) does George take than Harry to complete the math exercise.
an hour to complete the same exercise. How much more time (in fraction) does George take than Harry to complete the math exercise.
Solution
Time taken by George = 
Time taken by Harry = 
Time taken by George than Harry = 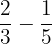
= 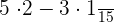
=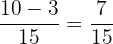
Hence, George takes 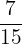 an hour more time than Harry to complete the math exercise.
an hour more time than Harry to complete the math exercise.
Example 7
Alice and her sister got the same amount of pocket money from their parents. Alice spent  of her pocket money on buying new toys. Her sister spent
of her pocket money on buying new toys. Her sister spent  of her pocket money on buying new books. How much more pocket money did Alice spend than her sister?
of her pocket money on buying new books. How much more pocket money did Alice spend than her sister?
Solution
Pocket money spent by Alice = 
Pocket money spent by her sister = 
To determine how much more pocket money Alice spent than her sister, we will subtract both the fractions like this:
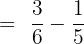
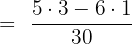
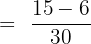
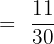
Hence, Alice spent 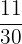 more money than her sister.
more money than her sister.













