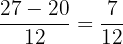Chapters
In this article, we will learn what are mixed fractions and how to solve problems when we are given fractions in their mixed forms. But before proceeding to discuss the mixed fractions, let us first see what is a fraction, how to write it and what are its types.

What is a Fraction?
A fraction represents parts of a whole or a collection
- Fraction of a whole: When a thing is divided into equal parts, then we represent the parts as a fraction of a whole. For example, consider a scenario in which a pizza is divided into four equal parts. The entire pizza is a whole and it is divided into four equal parts. Each part/piece is one-quarter of a whole and in fractional form is written as
 .
. - Fraction of a collection: Fraction of a collection reflects parts of a collection. For instance, Sam has 10 marbles. Out of 10 marbles, 7 are green and 3 are blue. The fraction of green marbles is seven-tenths and is mathematically written as
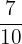 . The fraction of blue marbles in a collection is three-tenths and is mathematically written as
. The fraction of blue marbles in a collection is three-tenths and is mathematically written as 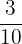 .
.
Fraction Notation
There are two parts/numbers in a fraction. The number above the line is known as a numerator and it depicts the number of equal parts of a whole or a set. The number below the line is known as the denominator and it reflects the number of equal parts a whole is divided into or the total number of elements in a set or a collection. For example, in a fraction  the numerator is 5 and the denominator is 4.
the numerator is 5 and the denominator is 4.
In the next section, we will discuss different types of fractions.
Types of Fractions
There are three types of fractions, proper, improper, and mixed fractions.
Proper Fractions
In a proper fraction, the numerator is always less than the denominator. For example,  ,
,  ,
,  are proper fractions because the number above the line, i.e. numerator is smaller than the number below the line, i.e. denominator. You will come across many proper fractions like
are proper fractions because the number above the line, i.e. numerator is smaller than the number below the line, i.e. denominator. You will come across many proper fractions like  ,
,  and
and  etc. The proper fractions which have 1 in the numerator are also known as unit fractions.
etc. The proper fractions which have 1 in the numerator are also known as unit fractions.
Improper Fractions
In an improper fraction, the numerator is greater than the denominator. For example,  ,
,  ,
,  are improper fractions because the number above the line, i.e. numerator is greater than the number below the line, i.e. denominator.
are improper fractions because the number above the line, i.e. numerator is greater than the number below the line, i.e. denominator.
Mixed Fractions
There are two parts in a mixed fraction or a mixed number. These parts are an integer or a whole number and a fractional part.
The examples of mixed fractions are 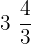 ,
, 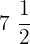 and
and 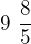 .
.
We can convert mixed fractions to an improper fraction and vice versa.
Converting Mixed Fraction to an Improper Fraction
Follow these steps to convert a mixed fraction to an improper fraction:
- Keep the denominator as it is.
- To get the number in the numerator, multiply the denominator with the whole number or integer part, and add numerator to it.
Consider the following example:
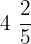 into an improper fraction.First, we will multiply the denominator 5 with 4 and then add 2 to it. The resulting number we will get is 22 which will be written in the numerator. The denominator will remain as it is. Hence, the improper fraction is:
into an improper fraction.First, we will multiply the denominator 5 with 4 and then add 2 to it. The resulting number we will get is 22 which will be written in the numerator. The denominator will remain as it is. Hence, the improper fraction is: 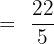
Converting an Improper Fraction to a Mixed Fraction
To convert an improper fraction to a mixed fraction, follow these simple steps:
- Divide the numerator by the denominator
- In the numerator of the fractional part, write the remainder
- In the whole number or an integer part of the mixed fraction, write the quotient.
- The denominator will be the same.
Consider the following example.
Convert 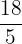 into a mixed fraction.
into a mixed fraction.
By dividing 18 by 5, we will get the quotient 3 and remainder 3. Thus the quotient will be the whole number or integer part of the mixed fraction and the remainder will be the numerator of the fractional part. The resulting mixed fraction will be:
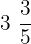
In the next section, we will solve some of the examples in which we will apply the arithmetic operations of addition, subtraction, multiplication, and division on mixed fractions.
Example 1
Solve 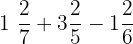
Solution
First, we will convert mixed fractions into improper fractions.
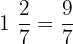
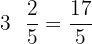
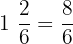
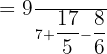
In the next step, we will take L.C.M (Least Common Multiple) also known as L.C.D (Least Common Divisor) of the numbers in the denominator. The denominators are 7, 5 and 6. Their L.C.M is 210.
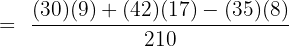
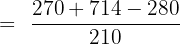
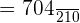
We can simplify the above fraction because both the numbers in the numerator and the denominator are multiples of 2.
=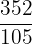
Example 2
Solve 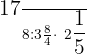
Solution
First, we will convert the above fractions into improper form:
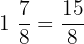
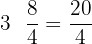
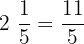
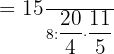
We have two operations in the above algebraic expression. One is division and the other is multiplication. We always invert the fractions and replace the division sign with multiplication first, if we have a division sign between them. After inverting we can multiply the fractions.
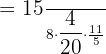
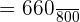
We can simplify the above fraction by dividing the numerator and denominator by 40:
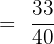
Example 3
A tailor is stitching the shirts and he had  of the total cloth left. To stitch every shirt, he uses
of the total cloth left. To stitch every shirt, he uses 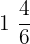 cloth. How many shirts can he stitch from the remaining cloth?
cloth. How many shirts can he stitch from the remaining cloth?
Solution
First, convert the mixed fractions to improper fractions.
Total cloth = 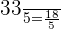
Cloth used in stitching a single shirt = 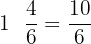
Number of shirts that can be stitched = 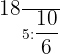
Since we have the ratio or division sign between both the fractions, therefore we will solve the fractions by replacing the division sign with multiplication and taking the reciprocal of the second fraction.
= 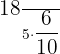
= 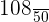
We will write the answer in simplified form by dividing the numerator and denominator by 2:
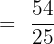 shirts
shirts
If we convert the above fraction into decimal point, then we will get the number 2.16. Hence, we can say that with the remaining cloth the tailor can stitch 2 shirts.
Example 4
Mariah spent  hours to complete her homework. Her friend Sarah took
hours to complete her homework. Her friend Sarah took 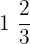 hours to complete her homework. How much more time (in fraction) did Mariah spend than Sarah in completing her homework?
hours to complete her homework. How much more time (in fraction) did Mariah spend than Sarah in completing her homework?
Solution
Time taken by Mariah = 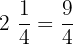
Time taken by Sarah = 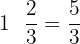
Additional time taken by Mariah (in fraction) = 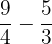
= 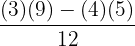
=