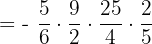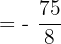Chapters
In this article, we will discuss the operations with fractions. But before discussing the operations, first, we will recall what are the fractions.
A fraction represents part of a whole or number of elements in a set. For instance, a pie is divided into 10 equal parts. Since the parts of the pie are equal, therefore each piece is represented by the fraction 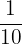 . It is an example of fractions representing equal parts of a whole.
. It is an example of fractions representing equal parts of a whole.
Consider another scenario in which your mother makes 7 pancakes. You get 4 out of 7, and your younger brother gets 3 out of 7 pancakes. The number of pancakes you got will be represented by the fraction  , whereas the number of pancakes your brother got is given by the fraction
, whereas the number of pancakes your brother got is given by the fraction  .
.
There are three types of fractions, proper, improper, and mixed fractions. A proper fraction has the numerator less than the denominator. An improper fraction has a numerator greater than the denominator. The mixed fraction or a mixed number has two parts- a whole number or integer part and a fractional part. The examples of three types of fractions are given below:
Proper fractions:  ,
, 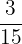 ,
, 
Improper fractions: 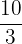 ,
, 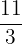 ,
, 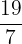
Mixed fractions: 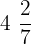 ,
, 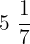 ,
, 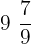
Mixed to Improper Fraction: We can convert mixed fractions to improper fractions and improper to mixed fractions. To convert a mixed fraction to an improper fraction, multiply the denominator with the whole number and add the numerator to it. The resulting number you get after multiplying and adding will be the numerator of the improper fraction. The denominator will remain the same.
Improper to Mixed Fraction: Follow a simple division process to convert the improper fraction to a mixed fraction. The quotient will be the whole number part of the mixed fraction and the remainder will be in the numerator. The denominator will remain the same.
We can apply arithmetic operations of addition, subtraction, multiplication, and division on fractions.
Addition and subtraction: If the denominators are the same, then we add or subtract the numerators and keep the denominator as it is. If the denominators are different, then we need to take the LCM of the numbers in the denominators. The denominator of each fraction is then divided by the LCM and we multiply the dividends with the corresponding numerators. The product of dividends and the numerators of both the fractions are written in the numerator along with the signs of addition or subtraction between them.
Multiplication: The numerator is multiplied with the numerator and the denominator is multiplied by the denominator.
Division: We flip the fraction after the division sign and replace the division sign with the multiplication one simultaneously. Flipping the fraction means taking the reciprocal of the fraction.

Operations with Fractions
You know that the order of operations on numbers is PEMDAS (Parenthesis, Exponents, Multiplication, Division, Addition, Subtraction). Like numbers, we also follow an order to solve fractions when multiple operations are involved. In the next section, we will discuss the order of operations on fractions.
Order of Operations on Fractions
If many operations are involved, then you should solve the fractions in the following order:
Step 1: Convert the mixed fractions and decimal numbers into the fractions.
Step 2: Carry out operations in the brackets, parentheses, and braces.
Step 3: Calculate the powers and roots
Step 4: Compute products and dividends from the left side
Step 5: Compute the addition and subtraction from the left side
Now, we will solve some of the examples of fractions in which multiples operations are involved.
Example 1
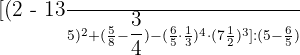
Solution
First, we will convert the mixed fractions to improper fractions:
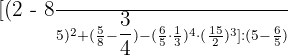
Now, we will compute the products within the parenthesis:
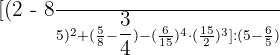
Now, we will carry out all other operations within the parenthesis:
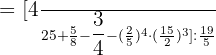
Compute the powers:
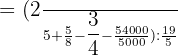
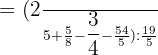
Carry out all the operations in the parenthesis on the left hand side of the algebraic equation:
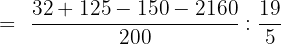
Add and subtract the numbers in the numerator, then divide and write the answer in simplified form:
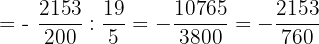
Example 2
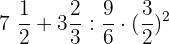
Solution
First, we will convert the mixed numbers to improper fractions:
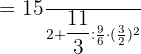
In the next step, we will calculate powers:
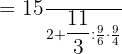
Now, we will flip the fraction after the division sign and replace it with the multiplication sign:
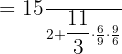
Apply the operation of multiplication from the left:
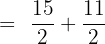
Add the above fractions by taking LCM. LCM stands for Least Common Multiple and is also known as least common divisor. It is the smallest number that can be evenly divided by both the numbers in the denominators.
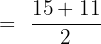
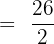

Example 3
Solve 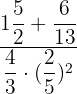
Solution
We can write the above expression as:
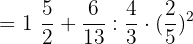
First, we need to convert the mixed fractions to improper fractions:
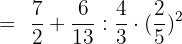
Now, we will calculate the powers:
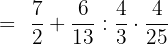
Now, we will multiply and divide from the left. For dividing, we need to change the sign and invert the fraction after the ":" sign. Inverting fraction means taking the reciprocal.
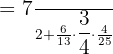
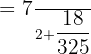
Now, we will add fractions by taking LCM.
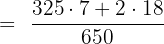
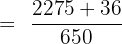
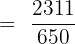
Example 4
Simplify 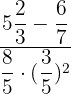
Solution
The expression in this example can be written as:
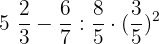
In the first step, we will convert the mixed fractions to imptoper fractions:
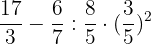
Now, we will compute the powers:
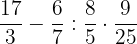
Now, starting from the left, we will multiply and divide. While dividing, it is necessary to flip the fraction after the division sign and replace the division sign with multiplication one.
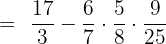
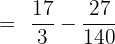
Subtract fractions by taking the LCM.
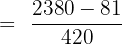
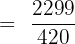
Example 5
Simplify 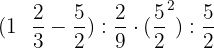
Solution
Convert the mixed numbers to improper fractions:
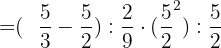
Solve the fractions in the paranthesis:
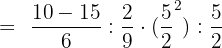
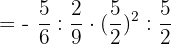
Calculate the powers:
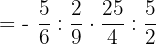
Multiply and divide fractions from the left: