Chapters
- Problem 1
- Problem 2
- Problem 3
- Problem 4
- Problem 5
- Problem 6
- Problem 7
- Problem 8
- Problem 9
- Problem 10
- Problem 11
- Problem 12
- Problem 13
- Problem 14
- Problem 15
- Problem 16
- Problem 17
- Problem 1 Solution
- Problem 2 Solution
- Problem 3 Solution
- Problem 4 Solution
- Problem 5 Solution
- Problem 6 Solution
- Problem 7 Solution
- Problem 8 Solution
- Problem 9 Solution
- Problem 10 Solution
- Problem 11 Solution
- Problem 12 Solution
- Problem 13 Solution
- Problem 14 Solution
- Problem 15 Solution
- Problem 16 Solution
- Problem 17 Solution

Problem 1
Write  as an addition of a series of fractional powers of
as an addition of a series of fractional powers of  and then as a series of simplified fractions.
and then as a series of simplified fractions.
Problem 2
Find the sum of
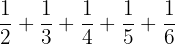
Problem 3
Try to find the product of
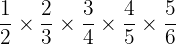
without performing the actual multiplication.
Problem 4
Solve the equation
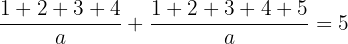
Problem 5
Solve the equation
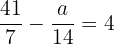
Problem 6
Find a Rational number in between
a.  and
and 
b.  and
and 
c. 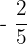 and
and 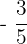
Problem 7
Divide  into
into  's and give each fractional value in both improper and mixed fractional form.
's and give each fractional value in both improper and mixed fractional form.
Problem 8
Divide  into
into 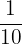 's and give each fractional value in both improper and mixed fractional form.
's and give each fractional value in both improper and mixed fractional form.
Problem 9
Divide the number line interval of  to
to  into 4 equal spaces and give the values of the endpoints of each space.
into 4 equal spaces and give the values of the endpoints of each space.
Problem 10
Divide the number line interval of  to
to  into 10 equal spaces and give the values of the endpoints of each space.
into 10 equal spaces and give the values of the endpoints of each space.
Problem 11
Name at least 4 Rational numbers that are between
a.  and
and 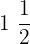
b.  and
and 
c.  and
and 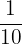
Problem 12
Solve:
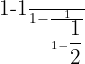
Problem 13
How many  's are in
's are in
a. 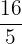
b. 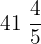
c. 
d. 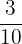
Problem 14
What is the fractional distance between these sets of points 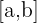 on the number line?
on the number line?
Interval 1: 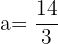 and
and 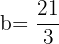
Interval 2: 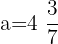 and
and 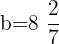
Interval 3: 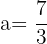 and
and 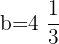
Interval 4: 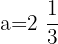 and
and 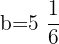
Problem 15
What is the midpoint of each of these intervals on the number line?
a. 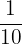 and
and 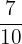
b. 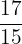 and
and 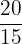
c.  and
and 
Problem 16
How many Rational numbers are there between 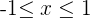 ?
?
Problem 17
What happens to the denominator and overall value of the Rational number  when
when
a.  is less than
is less than  but greater than
but greater than  and
and  is approaching
is approaching 
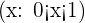
b.  is greater than
is greater than  but less than
but less than  and it is approaching
and it is approaching  (approaching
(approaching  from the negative side)
from the negative side)
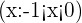
c.  is less than
is less than  and approaches
and approaches 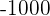
 and
and 
Problem 1 Solution
Write  as an addition of a series of fractional powers of
as an addition of a series of fractional powers of  and then again as a series of simplified fractions.
and then again as a series of simplified fractions.
Powers of  :
: 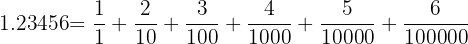
Simplified Fractions: 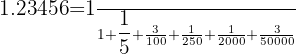
Problem 2 Solution
Find the sum of
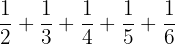
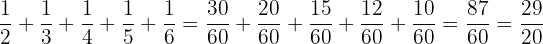
Problem 3 Solution
Try to find the product of
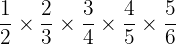
without performing the actual multiplication.
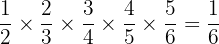
The denominator of each fraction cancels with the numerator of the fraction following it.
The denominator  in
in  cancels the numerator
cancels the numerator  in
in  etc.
etc.
The only 2 numbers that don't cancel are the numerator  in
in  and the denominator
and the denominator  in
in  leaving
leaving 
We can also rearrange the numerators to make 4 of the fractions equivalent to 
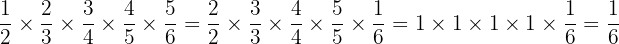
Problem 4 Solution
Solve the equation
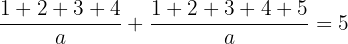
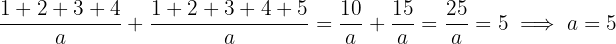
Problem 5 Solution
Solve the equation
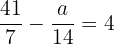
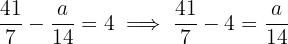
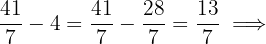
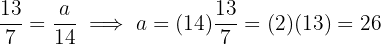
Problem 6 Solution
Find a Rational number in between
a.  and
and 
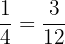 and
and 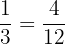
There is no fraction with a denominator of  between
between 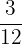 and
and 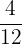 .
.
Converting denominators gives 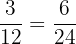 and
and 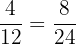
There is a fraction in between 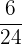 and
and 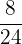 ,
,
namely 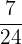
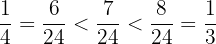
This is just one of infinitely many fractions between  and
and  .
.
b.  and
and 
 and
and 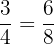
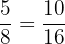 and
and 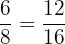
There is a fraction between 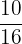 and
and 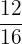 ,
,
namely 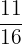 .
.
c. 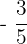 and
and 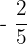
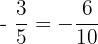 and
and 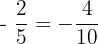
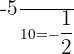
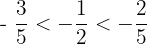
Problem 7 Solution
Divide  into
into  's and give each fractional value in improper and mixed fraction form.
's and give each fractional value in improper and mixed fraction form.
Interval 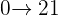 into
into 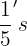
1. 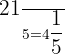
2. 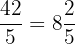
3. 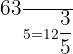
4. 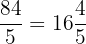
5. 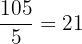
Problem 8 Solution
Divide  into
into 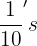 and give each fractional value in both improper and mixed form.
and give each fractional value in both improper and mixed form.
Interval 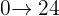 into
into 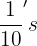
1. 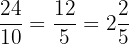
2. 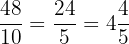
3. 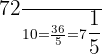
4. 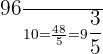
5. 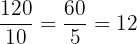
6. 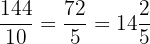
7. 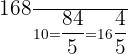
8. 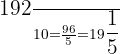
9. 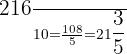
10. 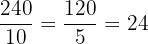
Problem 9 Solution
Divide the number line interval of  to
to  into
into 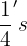 and give each value.
and give each value.
Number Line Distance: 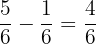
Spaces: 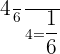
Interval 1: 
Interval 2: 
Interval 3: 
Interval 4: 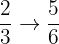
Problem 10 Solution
Divide the number line interval of  to
to  into
into 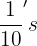 and give each value.
and give each value.
Number Line Distance: 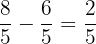
Spaces: 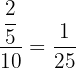
Number Line Start and Finish: 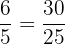 and
and 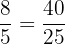
Interval 1: 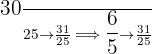
Interval 2: 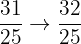
Interval 3: 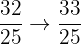
Interval 4: 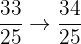
Interval 5: 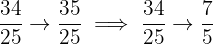
Interval 6: 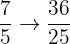
Interval 7: 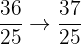
Interval 8: 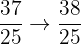
Interval 9: 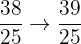
Interval 10: 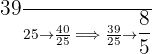
Problem 11 Solution
Name at least 4 Rational numbers that are between
a.  and
and 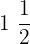
Here are quite a few Rational numbers between  and
and 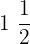
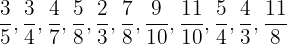
b.  and
and 
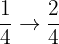
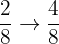
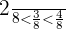
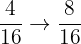
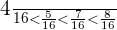
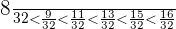
c.  and
and 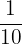
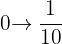
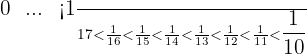
Problem 12 Solution
Solve:
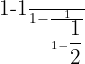
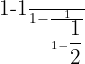
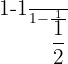
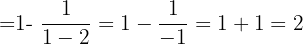
Problem 13 Solution
How many  's are in
's are in
a. 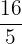
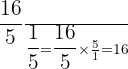
b. 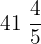
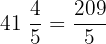
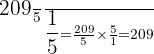
c. 
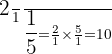
d. 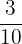
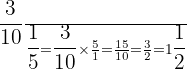
Problem 14 Solution
What is the fractional distance  between these sets of points
between these sets of points 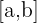 on the number line?
on the number line?
Interval 1: 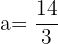 and
and 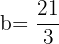
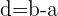
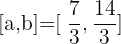
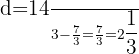
Interval 2: 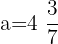 and
and 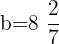
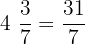 and
and 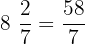
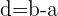
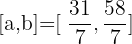
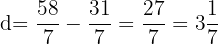
Interval 3: 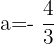 and
and 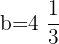
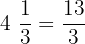
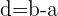
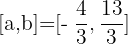
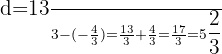
Interval 4: 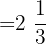 and
and 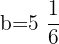
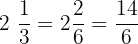 and
and 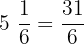
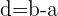
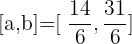
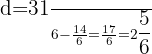
Problem 15 Solution
What is the midpoint  of each of these intervals on the number line?
of each of these intervals on the number line?
a. 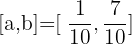
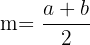
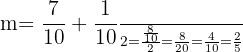
b. 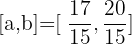
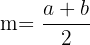
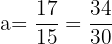 and
and 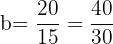
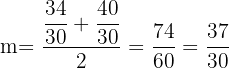
c. 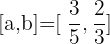
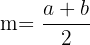
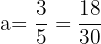 and
and 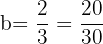
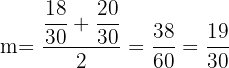
Problem 16 Solution
How many Rational numbers  are there between
are there between 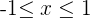 ?
?
There are an infinite amount of Rational numbers in between any 2 other Rational numbers.
Problem 17 Solution
What happens to the denominator and overall value of the Rational number  when
when
a.  is less than
is less than  but greater than
but greater than  and
and  is approaching
is approaching 
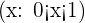 with
with  or
or 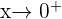
The Rational number  gets bigger and bigger as
gets bigger and bigger as  .
.
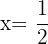 and
and 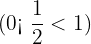 gives
gives 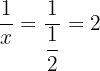
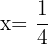 and
and 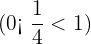 gives
gives 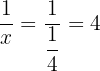
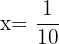 and
and 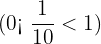 gives
gives 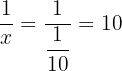
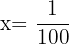 and
and 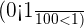 gives
gives 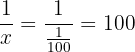
b.  is greater than
is greater than  but less than
but less than  and
and  is approaching
is approaching  (approaches
(approaches  from the negative side)
from the negative side)
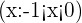 with
with  or
or 
The Rational number  gets bigger and bigger negatively as
gets bigger and bigger negatively as  .
.
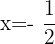 and
and 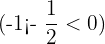 gives
gives 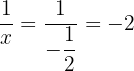
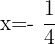 and
and 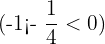 gives
gives 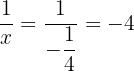
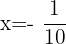 and
and 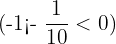 gives
gives 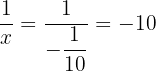
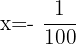 and
and  gives
gives 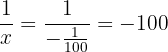
c.  is less than
is less than  and approaches
and approaches 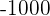
 and
and 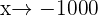
The Rational number  gets smaller and smaller negatively as
gets smaller and smaller negatively as 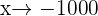 .
.
 and
and 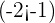 gives
gives 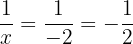
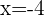 and
and  gives
gives 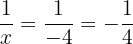
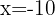 and
and 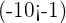 gives
gives 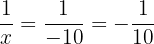
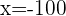 and
and  gives
gives 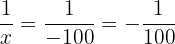
Summarise with AI:












