Chapters

What is a Fraction?
We represent equal parts of a whole or a collection using a fraction. We use the fraction of a whole when we are dealing with objects/elements divided into equal parts. For instance, if a pie is divided into 2 equal parts, then we will represent each half by the fraction  . Similarly, if we will divide it into four equal parts, then each quarter will be represented by the fraction
. Similarly, if we will divide it into four equal parts, then each quarter will be represented by the fraction  .
.
On the other hand, the fraction of a collection means parts of a collection. For example, suppose you have 13 chocolates and you give 9 to your younger brother and the remaining to your friend. The fraction of chocolates given to your younger brother is 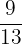 and the fraction of chocolates given to your friend is
and the fraction of chocolates given to your friend is 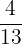 .
.
How to Write Fractions?
A fraction has two parts or numbers. A number above the line is called a numerator and the number below the line is known as the denominator. A numerator shows the number of elements you have. The denominator represents the total number of elements in a collection or number of equal parts into which an object is divided into. For example, in a fraction,  3 is the numerator and 8 is the denominator.
3 is the numerator and 8 is the denominator.
Types of Fractions
There are three kinds of fractions, proper, improper, and mixed fractions. The types of fractions along with the examples are explained below:
Proper Fractions
In these fractions, the numerator is less than the denominator. For example,  ,
,  , and
, and  are proper fractions. The fractions that have 1 in the numerator are called unit fractions. The examples of unit fractions include
are proper fractions. The fractions that have 1 in the numerator are called unit fractions. The examples of unit fractions include  ,
,  , and
, and  .
.
Improper Fractions
In these fractions, the numerator is greater than the denominator. For example,  ,
,  , and
, and  are improper fractions.
are improper fractions.
Mixed Fractions
These fractions have two parts - a whole number or integer part and a fractional part. These fractions are also known as mixed numbers. For example, 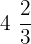 ,
, 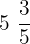 , and
, and 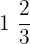 are mixed fractions. In these fractions, the integers or whole number are 4, 5 and 1. The improper fractions can be converted to mixed fractions and vice versa.
are mixed fractions. In these fractions, the integers or whole number are 4, 5 and 1. The improper fractions can be converted to mixed fractions and vice versa.
In the next section, we will discuss how to convert the fractions into equivalent fractions having a common denominator.
Common Denominator
While adding or subtracting fractions, the denominators must be equal. In other words, we can say that all the fractions should have a common denominator. Sometimes, we have the fractions having the same denominators. In these cases, adding or subtracting fractions is easy as all we have to do is keeping the denominator the same, and adding or subtracting the numbers is the numerators.
In majority of the problems, we get fractions that have different denominators. In these cases, for adding and subtracting fractions, we need to convert the fractions into equivalent fractions that have the same denominators.
How to Make the Denominators Same?
In this method, we multiply the numerator and denominator of a fraction by the denominator of other fractions. Once we obtain the fractions with the same denominators, we solve them like we solve the fractions with the same denominators.
Example 1
Solve the following fractions using a common denominator method.
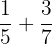
Solution
The denominator of the first fraction is 5 and the second fraction is 7. We will multiply 5 with the second fraction  and 7 with the first fraction
and 7 with the first fraction  . The resulting fractions will be:
. The resulting fractions will be:
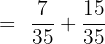
The above fractions have the same denominator, therefore we will simply add the numerators and keep the denominator as it is.
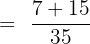
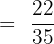
Example 2
Solve the following fractions by finding the common denominator.
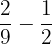
Solution
In the denominator of the first fraction, we have 9 and in the second fraction we have 2. We will multiply 9 with the second fraction  and 2 with the first fraction
and 2 with the first fraction  . The resulting fractions will be:
. The resulting fractions will be:
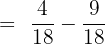
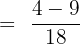
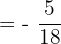
Example 3
Use the common denominator method to solve the following fractions.
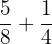
Solution
The denominator of the first fraction is 8 and the second fraction is 4. We will multiply 8 with the second fraction  and 4 with the first fraction
and 4 with the first fraction  . The resulting fractions will be:
. The resulting fractions will be:
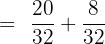
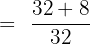
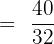
The fractions can be simplified further because both the numbers in the numerator and the denominators are multiples of 8.
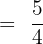
Example 4
Add fractions below using a common denominator method.
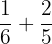
Solution
The denominator of the first fraction is 6 and the second fraction is 5. We will multiply 6 with the second fraction  and 5 with the first fraction
and 5 with the first fraction  . The resulting fractions will be:
. The resulting fractions will be:
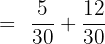
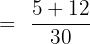
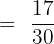
Example 5
Solve the following fractions using a common denominator method.
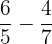
Solution
The denominator of the first fraction is 5 and the second fraction is 7. We will multiply 5 with the second fraction  and 7 with the first fraction
and 7 with the first fraction  . The resulting fractions will be:
. The resulting fractions will be:
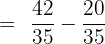
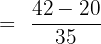
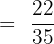
Least Common Denominator Method
We can use another method to solve fractions when we have to add or subtract fractions with different denominators. This method entails finding a Least Common Denominator or LCM (Least Common Multiple) to solve fractions.
The least common denominator has the following attributes:
- The least common denominator is the Least Common Multiple (LCM) or Least Common Divisor (LCD) of the numbers in the denominators.
- The least common denominator is the smallest number which can be easily divisible by both the denominators.
- We solve the fractions by dividing each denominator by the common divisor and multiplying the quotient obtained by the corresponding numerators.
Example 1
Solve the following fractions using the least common denominator method:
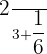
Solution
We have to find the least common denominator of 3 and 6 to solve this example. The least common denominator is also known as LCM (Least Common Multiple). To compute the LCM, let us write the multiples of 3 and 6 like this:
Multiples of 3 = 3, 6, 9, 12, 15, 18, ....
Multiples of 6 = 6, 12, 18, 24, 36,....
The least common multiple of both the numbers is 6. In other words, it is the smallest number that can be evenly divided by both numbers in the denominators. After finding the least common multiple, we will proceed to the next step which entails dividing each denominator with LCM and multiplying the dividend with the corresponding numerators followed by addition or subtraction.
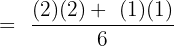
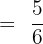
Example 2
Add and subtract the following fractions using the least common denominator method.
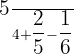
Solution
We have to find the least common denominator also known as LCM of 4, 5, and 6 to solve this example. To compute the LCM, let us write the multiples of 4, 5 and 6 like this:
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60,...
Multiples of 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, ....
Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ....
The least common multiple of all the three numbers is 60. In other words, it is the smallest number that can be evenly divided by both numbers in the denominators. Instead of writing the multiples, we can also find LCM by writing the numbers in the denominators on the right hand side of the table and writing divisors on the left hand side. In the end, we multiply all the numbers on the left hand side to get LCM.
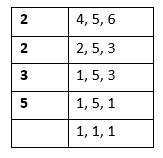
LCM = 2 x 2 x 3 x 5 = 60
After finding the least common multiple, we will proceed to the next step which entails dividing each denominator with L.C.M and multiplying the dividend with the corresponding numerators:
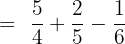
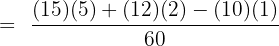
After multiplication, we will get the following expression:
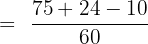
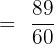
Simplifying the above fraction is not possible because we cannot divide 89 and 60 by the same number.
Find more Maths teacher here on Superprof.
Summarise with AI:













