Chapters

Collinear Points Definition

| Definition | Possible Directions | Form | Example | |
| Coordinate | A set of numbers that allows you to locate a point on a plane | Left (-) or right (+); Up (+) or down (-) | (x,y) | (2,4) |
Let’s break down the meaning of collinear:
| Co- | Together |
| Linear | Related to a line |
Collinear is, then, to be together on a line.
| Two points | Always collinear |
| Three or more points | Sometimes collinear |
Example of Collinear Points
As seen in the previous section, two points are always collinear. This is because any two points will always form a line. Take some examples below.

| A | Collinear |
| B | Collinear |
The real trick is when we have three or more points. If we are dealing with 3+ points, we will have to check whether or not they are collinear. Take some examples below.

| A | Collinear |
| B | Not Collinear |
Prove 3 Points are Collinear
There are two ways that you can prove that 3 points are collinear. Take a look at a summary of the methods below.
| Description | |
| Slope Method | Use the slope of the points to find if they are collinear |
| Area Method | Use the area of the triangle formed by the points |
Method 1
As we saw in the previous section, the first method to prove if three points are collinear is to use the slope method. In order to use this method, you should know what a slope is.
Every line has a slope, and since two points make a line, it follows that any time you have two or more points you also have a slope.
| Slope-intercept formula for a line | y=mx+b |
| (x,y) | Any point on the line |
| m | The slope |
| b | The y-intercept |
When three points are collinear, the slope of any of the pairs of those three points are the same. Take a look.

When we have three points, we have three different lines:
| Line 1 | Between A and B | AB |
| Line 2 | Between B and C | BC |
| Line 3 | Between A and C | AC |
As in the picture, if three points are collinear, or on the same line, then their slopes will be the same.
Slope Formula
In order to use the slope method, you should know the formula of the slope of a line. Take a look below.
| Formula for the slope | 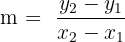 |
| Point 1 |  |
| Point 2 |  |
As you can see, the formula for the line is quite simple. When we have two points  and
and 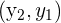 , the slope that they form is simply the second y coordinate minus the first y coordinate divided by the two x coordinates subtracted from one another.
, the slope that they form is simply the second y coordinate minus the first y coordinate divided by the two x coordinates subtracted from one another.
Example Method 1
Let’s say we have three points, listed below.
| Point A | (1,3) |
| Point B | (5,15) |
| Point C | (10,30) |
Let’s use the slope method to find out whether or not they are collinear. In order to use this method, we simply need to pick two points and find the slope between them. For practice, let’s find the slopes of every line that they form.
| Line | Slope |
| AB | 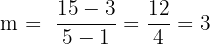 |
| BC | 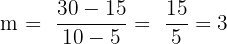 |
| AC | 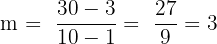 |
As we can see, the points are collinear.

Method 2
The second method is a tiny bit more complicated. Let’s start with the basic concept below.
| 3 collinear points | Form a straight line |
| 3 non-collinear points | Form a triangle |
As you can see, when three points are not collinear, they form a triangle, no matter how far or close apart the points are.
In this method, we check the area of the ‘triangle’ formed by the three points. Take a look at the steps you should follow below.
| Step 1 | Plug the three points into the area equation for a triangle formed by three points |
| Step 2 | If the area = 0, then the points form a straight line. This makes sense: a triangle with an area of zero is simply a line |
| Step 3 | If the area < 0, then the points form a triangle and they are not collinear |
Area of a Triangle
When we’re trying to find the area of a triangle, it depends on what type of triangle we’re working with. If we know the height and base of the triangle, we can simply use the regular area of a triangle formula.
However, since we’re working with coordinates, the easiest way is to use the area of a triangle for three points, or coordinates. Take a look below.

| Point 1 |  |
| Point 2 |  |
| Point 3 |  |
The area formula is written below.
| Area of Triangle | 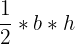 |
| Area of Triangle with 3 Points | 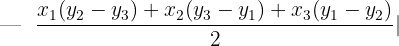 |
Example Method 2
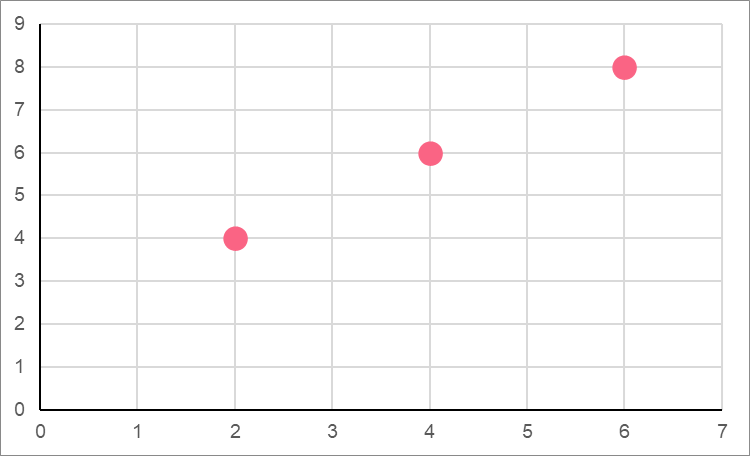
Let’s go through a step-by-step example of how to find if two points are collinear using the area method. Say you have the following points.
| Point 1 |  | (2,4) |
| Point 2 |  | (4,6) |
| Point 3 |  | (6,8) |
Let’s plug them into the formula.
\[
| \frac{ 2(6 - 8) + 4(8 - 4) + 6(4 - 6) }{2} |
\]
Simplify the values.
\[
| \frac{ (-4) + (16) + (-12) }{2} | = \frac{0}{2} = 0
\]
When we plot these numbers, we can see that they indeed form a straight line.