Chapters
In this article, we will discuss the concept of absolute value in detail.

What is an Absolute Value?
Absolute value can be defined as:
"The distance at which any number is located from zero. For example, the absolute value of a will be |a|"
The symbol "||" is used to depict the absolute value of a number. The absolute value concept is very important and useful in many areas like calculating the distance between two real numbers.
The absolute value of a positive or negative number is always positive. For instance, we know that the absolute value of 7 is equal to 7 because the distance between 0 and 7 is 7. Can you tell what is the absolute value of -7? Well, the absolute value of -7 will be also 7 because the distance between 0 and -7 is also 7. Mathematically, we can write these examples as:
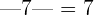

The absolute value of 0 is 0.
We have already discussed that whether the number is positive or negative, the absolute value of the number is a number itself with a positive sign. However, when we have a variable inside the absolute value function, the value of the variable can be positive or negative. Hence, we have two possibilities in these kinds of equations. For example, consider the following equation, in which we have a variable inside an absolute value function on the left hand side.
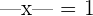
The value of x can be 1 or -1. In both cases, the result will be the same.
 or
or 
Calculating distance from absolute value
We can use the absolute value to compute the distance between two real numbers a and b. For instance, if you are asked to calculate the distance between two real numbers a and b, then you need to take the absolute value of the difference of b and a to get the distance.
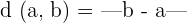
Consider the following example:
Calculate the distance between 9 and -3.
To calculate the distance, we will substitute the values of a and b in the formula below:
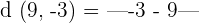
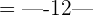
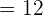
Hence, the distance between 9 and -3 is 12 units. In other words, we can say that 9 and -3 are 12 units apart.
In the next section, we will discuss some of the properties of absolute value.
Properties of the Absolute Value
- The numbers that are opposite to each other have the same absolute value. It means that the same value with a positive or negative sign will have the same absolute value. For instance, consider the following examples.
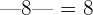 and
and 
 and
and 
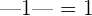 and
and 
- The product's absolute value is equal to the product of the absolute values of the terms. For instance, the absolute value of the product of two factors a and b is equal to the absolute value of a multiplied by the absolute value of b. Mathematically, we can denote it as:

Consider the following examples:
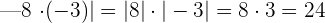

- The absolute value of the sum of two factors is less than or equal to the sum of the absolute values of the factors. Mathematically, we can denote this property as:

Consider the following examples:


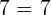
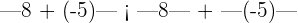
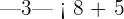
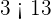
In the next section, we will solve some examples related to the absolute value.
Example 1
Simplify - |-4|.
Solution
We know that the absolute value of a negative number is also a positive number. Hence, the absolute value of -4 is 4. The negative sign before the absolute value will remain as it is:
- |-4|
- 4
Example 2
Simplify  .
.
Solution
The absolute value of the product is equal to the product of the absolute value of individual terms. In this example, the absolute value of 9 into 2 is equal to the product of the absolute value of 9 and absolute value of 2.


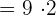
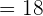
Example 3
Simplify 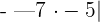 .
.
Solution
The absolute value of the product is equal to the product of the absolute value of individual terms. In this example, the absolute value of 7 into -5 is equal to the product of the absolute value of 7 and the absolute value of -5.
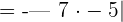
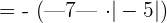
The absolute value of 7 is 7 and the absolute value of -5 will be 5.

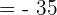
Example 4
What is the distance between -6 and 18?
Solution
To compute the distance between these two numbers, we need to substitute the values in the formula below:
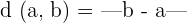
In this example, the value of b is 18 and the value of a is -6.
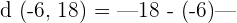


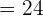
Hence, the distance between the numbers -6 and 18 is 24 units or we can say that the numbers -6 and 18 are 24 units apart.
Example 5
What is the distance between -482 and 166?
Solution
To compute the distance between these two numbers, we need to substitute the values in the formula below:
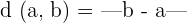
In this example, the value of b is 166 and the value of a is -482.

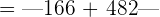


Hence, the distance between the numbers -482 and 166 is 648 units or we can say that the numbers -482 and 166 are 648 units apart.
Example 6
Solve 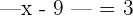
Solution
In this example, we need to calculate the value of x. Since the value of x is unknown, hence when the absolute value sign will be removed, we will get two results.

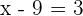 or
or 
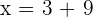 or
or 
 or
or 
Hence, the values of x are either 6 or 12. When you will substitute these values of x in the original function, the result will be the same.
At x = 12, 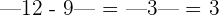
At x = 6, 
Example 7
Solve 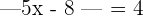
Solution
In this example, we need to calculate the value of x. Since the value of x is unknown, hence when the absolute value sign will be removed, we will get two results.
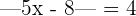
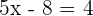 or
or 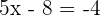
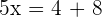 or
or 
 or
or 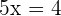
 or
or 
Hence, the values of x are either 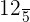 or
or  . When you will substitute these values of x in the original function, the result will be the same.
. When you will substitute these values of x in the original function, the result will be the same.
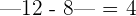
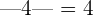
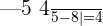

Example 8
Solve 
Solution
In this example, we need to calculate the value of x. Since the value of x is unknown, hence when the absolute value sign will be removed, we will get two results.

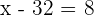 or
or 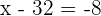
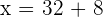 or
or 
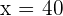 or
or 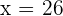
Hence, the values of x are either 26 or 40. When you will substitute these values of x in the original function, the result will be the same.
At x = 40, 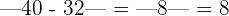
At x = 26, 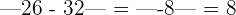
Example 9
Solve 
Solution
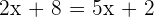 or
or 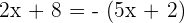
 or
or 
 or
or 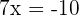
 or
or 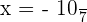
Hence, the values of x is either 2 or  .
.













