Chapters

Integer
In order to understand radicals, you should first know what an integer is. An integer is part of a group of numbers known as real numbers. There are two main types of numbers that are not real numbers:
- Imaginary numbers
- Infinity
Remember, these are not real numbers. You are probably more familiar with real numbers, which include:
- Whole numbers
- Rational numbers
- Irrational numbers
Take a look at the image and table below to better understand the difference between these two types of numbers.

| Description | More examples | |
| Whole | Positive real number without decimal/fraction | 188, 7 000 |
| Rational | Positive or negative with decimal/fraction | 1.1, -888.99 |
| Irrational | Positive or negative, can’t be written as decimal/fraction | 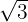 , ,  |
You may be wondering, what happens when you have a negative whole number? That is actually an integer.
Real Number
Real numbers are the basis of most of the maths you will learn or use. Whenever you’re in doubt, it can be helpful to look at a number line, also called a “real number line.”

Exponents
We’re almost to radicals. One last concept to understand before diving into radicals is that of an exponent. An exponent can be thought of as the opposite of a radical. Another name for exponents is ‘powers.’ The table below describes some exponents.
| Meaning | Common Name | Written | |
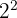 | 2 x 2 | Square | Two to the power of 2; Two squared |
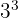 | 3 x 3 x 3 | Cube | 3 to the power of 3; 3 cubed |
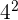 | 4 x 4 | Square | 4 to the power of 2; 4 squared |
Radical Definition
Recall that a radical, also called a ‘root,’ is the opposite of an exponent. Because of this, you can think of each operation as ‘undoing’ the other. Let’s first go through the most common radical: the square root.
| Square Root | Result | Written | |
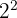 = 4 = 4 | 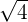 , ,  | 2 | Square root of 2 |
 = 49 = 49 | 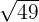 , ,  | 7 | Square root of 3 |
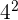 = 16 = 16 |  , , 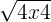 | 4 | Square root of 2 |
Notice what the operations in the table have in common? The square roots are all ‘undoing’ powers of 2. In other words, the square root takes any number and tries to find what number ‘fits’ exactly twice when multiplied by itself.
When you want to take the nth root of a number x, it means you want to find the number k that, multiplied by itself n times, will give you the original number x.

| Square Root | Result | Result | |
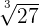 | 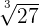 = k * k * k = k * k * k |  | 3 |
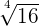 | 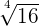 = k * k * k * k = k * k * k * k | 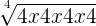 | 4 |
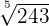 | 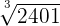 = k * k * k * k * k = k * k * k * k * k |  | 5 |
Notation of Radicals
Radicals have some common notations. The first thing you should note is that a radical can actually be written as an exponent. Take a look below.

| Explanation | Example | |
 = = 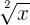 | A square root is simply a number to the 2nd root, because they are the most common the 2 is usually not written | 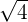 = =  |
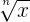 | A number to the nth root | 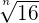 |
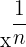 = = 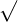 | A number to the nth root can also be written as an exponent, which is 1 over the nth root | 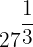 = = 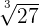 |
Radical Example
Let’s take a look at some examples of radicals. Let's complete the following task: convert the sentence into the common notation for the radical.
- The 4th root of 16
- The square root of 225
- 4 to the power of
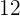
After this, solve the problem. These kinds of problems are often solved by calculators, which usually have the square root symbol and a separate symbol: 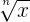 .
.

Radical Rules
There are a couple of rules you should keep in mind when you’re dealing with radicals. These rules are written in the table below, along with their descriptions.
| Rule | Example |
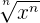 = x = x | 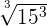 = 15 = 15 |
 = = 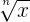 * *  |  = = 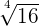 * *  = 2*3 = 6 = 2*3 = 6 |
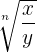 = = 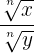 | 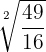 = \frac{ = \frac{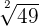 }{ }{ } = } =  |
 * * = x = x |  * * = 400 = 400 |
Radical Simplification
There are many ways that you can simplify a radical. The most common way you can try to simplify a radical is to try and divide the number up inside of the radical so that you can get a perfect square.
A perfect square is a radical that contains a number that can be simplified into a square. Take four as an example.

To simplify larger radicals, you can apply the same approach. Take the number 20 as an example.
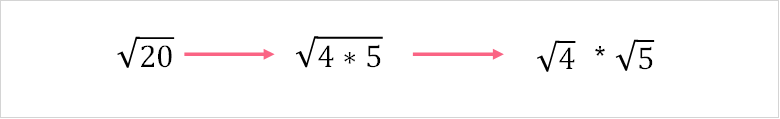
- Break down the original number
- See if there are any perfect squares
- We are left with 2 *

Radical Division
In order to simplify radical division, we need to use a combination of the rules we learned above. First, we have the following.
\[
\sqrt{\frac{4}{32}}
\]
We use the rules above to solve by first rewriting it, then splitting it into smaller numbers.
\[
\frac{\sqrt{4}}{\sqrt{16*2}} = \frac{\sqrt{2^2}}{\sqrt{4^2} * {\sqrt{2}}} = \frac{2}{4*{\sqrt{2}}}
\]
Simplifying the nominator and denominator, we simply get:
\[
\frac{1}{2*{\sqrt{2}}}
\]













