Chapters

Real number
While it may seem like we only have and use one type of number in our daily lives, there are actually many different types of numbers. Take a look at some of the numbers in the image below.

- Whole numbers
- Integers
- Rational numbers
- Irrational numbers
To understand what these different types of numbers are, take a look at the table below.
| Examples | Definition | |
| Whole | 0, 5, 65, 100, 788 | Positive numbers that are not fractions or decimals |
| Integer | -5, -75, -340, -800, 55, 90 | Positive and negative numbers that aren’t fractions or decimals |
| Rational |  , 0.67 , 0.67 | A number that is made from the division of two integers |
| Irrational |  , ,  | A number that can’t be written as a fraction or decimal |
Number Line
In order to better understand the differences between these different types of numbers, it can be helpful to use a number line. A number line can help you identify what types of numbers you’re dealing with. Take the following set of numbers as an example, which give 5 numbers. Let’s see if we can figure out what kind of number they are.
| Number | Type | |
| 1 | 3.3 | ? |
| 2 | 5 | ? |
| 3 | -6 | ? |
| 4 | -5.3 | ? |
| 5 | 1.4142135623….. | ? |
A number line is a plot of numbers on a straight line. We can use a number line to help us decide what kind of numbers we have. Take the following as an example.


| Number | Type | Why | |
| 1 | 3.3 | Rational | A number that is made by dividing 33 by 10 |
| 2 | 5 | Whole | A positive number that’s not a decimal |
| 3 | -6 | Integer | A negative number that’s not a decimal |
| 4 | -5.3 | Rational | A number made by dividing -53 by 10 |
| 5 | 1.4142135623….. | Irrational | A number that can’t be written as a fraction |
Irrational Number
As stated in the first section, an irrational number is different from a rational number. While a rational number is any number that can be written as a decimal or a fraction, an irrational number can’t be expressed as a ratio of two integers. Find some examples in the table below.
| In Decimal or Fraction Form | Description | |
5 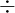 10 10 | 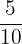 | A ratio of 5 to 10 |
| .0066 | 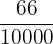 | A ratio of 66 to 10 000 |
 | 1.7320508075688772... | Cannot be expressed as a ratio |
Generally, there are many roots that are irrational numbers. Recall that roots can be squares, cube and more. However, keep in mind that not all roots are irrational numbers. Take the following examples:
| Result | Type | |
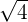 | 2 | Rational |
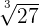 | 3 | Rational |
 | 4.3267487109... | Irrational |
Examples
In this section, we’ll go over some examples of irrational numbers. These irrational numbers are the ones you are likely to encounter in other classes, as they are very famous.
Pi
Pi is the most common example of an irrational number. It is represented by the Greek letter pi:


| Fraction | Decimal |
| 22/5 | 4.4 |
| 22/6 | 3.666667 |
| 22/7 | 3.142857 |
| 22/8 | 2.75 |
Euler’s Number
Euler’s number is the second most common irrational number that you’ll encounter in math. Euler’s number is similar to pie in that it can be calculated to many decimal places but still does not show any pattern, or any sign of stopping.
Euler’s number is written as an  , which can be seen below.
, which can be seen below.

| Description | Example | |
| Euler’s | Using only  | 5 *  , ,  |
| Natural Base | Using it as a base for a logarithm | 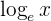 |
When we use Euler’s number as the natural base, we can call the logarithm a natural logarithm, which is written as  .
.

| Example | |
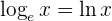 |  |
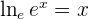 | 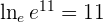 |
Golden Ratio
The golden ratio is represented by the Greek letter 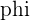 and can be found in many different aspects of life. It can often be found in art and architecture. To find the golden ratio, let’s start with a rectangle.
and can be found in many different aspects of life. It can often be found in art and architecture. To find the golden ratio, let’s start with a rectangle.

This sounds a bit complicated, but we can try with an example.

| Result | |
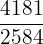 | 1.6180341 |
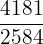 | 1.6180341 |
As you can see, this approximates the golden ratio.













